Figure 1: A regular 3-layer Neural Network.
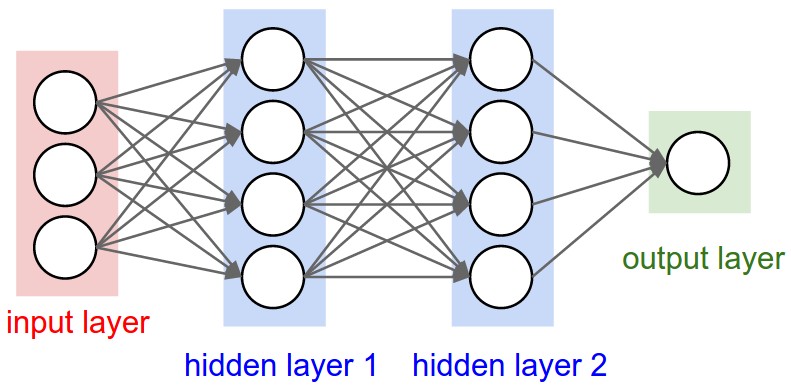
Artificial neural networks are computational systems that can learn to perform tasks by considering examples, generally without being programmed with any task-specific rules. It is supposed to mimic a biological system, wherein neurons interact by sending signals in the form of mathematical functions between layers. All layers can contain an arbitrary number of neurons, and each connection is represented by a weight variable.
The field of artificial neural networks has a long history of development, and is closely connected with the advancement of computer science and computers in general. A model of artificial neurons was first developed by McCulloch and Pitts in 1943 to study signal processing in the brain and has later been refined by others. The general idea is to mimic neural networks in the human brain, which is composed of billions of neurons that communicate with each other by sending electrical signals. Each neuron accumulates its incoming signals, which must exceed an activation threshold to yield an output. If the threshold is not overcome, the neuron remains inactive, i.e. has zero output.
This behaviour has inspired a simple mathematical model for an artificial neuron. $$ \begin{equation} y = f\left(\sum_{i=1}^n w_ix_i\right) = f(u) \label{artificialNeuron} \end{equation} $$ Here, the output \( y \) of the neuron is the value of its activation function, which have as input a weighted sum of signals \( x_i, \dots ,x_n \) received by \( n \) other neurons.
Conceptually, it is helpful to divide neural networks into four categories:
In quantum information theory, it has been shown that one can perform gate decompositions with the help of neural.
The applications are not limited to the natural sciences. There is a plethora of applications in essentially all disciplines, from the humanities to life science and medicine.
An artificial neural network (ANN), is a computational model that consists of layers of connected neurons, or nodes or units. We will refer to these interchangeably as units or nodes, and sometimes as neurons.
It is supposed to mimic a biological nervous system by letting each neuron interact with other neurons by sending signals in the form of mathematical functions between layers. A wide variety of different ANNs have been developed, but most of them consist of an input layer, an output layer and eventual layers in-between, called hidden layers. All layers can contain an arbitrary number of nodes, and each connection between two nodes is associated with a weight variable.
Neural networks (also called neural nets) are neural-inspired nonlinear models for supervised learning. As we will see, neural nets can be viewed as natural, more powerful extensions of supervised learning methods such as linear and logistic regression and soft-max methods we discussed earlier.
The feed-forward neural network (FFNN) was the first and simplest type of ANNs that were devised. In this network, the information moves in only one direction: forward through the layers.
Nodes are represented by circles, while the arrows display the connections between the nodes, including the direction of information flow. Additionally, each arrow corresponds to a weight variable (figure to come). We observe that each node in a layer is connected to all nodes in the subsequent layer, making this a so-called fully-connected FFNN.
A different variant of FFNNs are convolutional neural networks (CNNs), which have a connectivity pattern inspired by the animal visual cortex. Individual neurons in the visual cortex only respond to stimuli from small sub-regions of the visual field, called a receptive field. This makes the neurons well-suited to exploit the strong spatially local correlation present in natural images. The response of each neuron can be approximated mathematically as a convolution operation. (figure to come)
Convolutional neural networks emulate the behaviour of neurons in the visual cortex by enforcing a local connectivity pattern between nodes of adjacent layers: Each node in a convolutional layer is connected only to a subset of the nodes in the previous layer, in contrast to the fully-connected FFNN. Often, CNNs consist of several convolutional layers that learn local features of the input, with a fully-connected layer at the end, which gathers all the local data and produces the outputs. They have wide applications in image and video recognition.
So far we have only mentioned ANNs where information flows in one direction: forward. Recurrent neural networks on the other hand, have connections between nodes that form directed cycles. This creates a form of internal memory which are able to capture information on what has been calculated before; the output is dependent on the previous computations. Recurrent NNs make use of sequential information by performing the same task for every element in a sequence, where each element depends on previous elements. An example of such information is sentences, making recurrent NNs especially well-suited for handwriting and speech recognition.
There are many other kinds of ANNs that have been developed. One type that is specifically designed for interpolation in multidimensional space is the radial basis function (RBF) network. RBFs are typically made up of three layers: an input layer, a hidden layer with non-linear radial symmetric activation functions and a linear output layer (''linear'' here means that each node in the output layer has a linear activation function). The layers are normally fully-connected and there are no cycles, thus RBFs can be viewed as a type of fully-connected FFNN. They are however usually treated as a separate type of NN due the unusual activation functions.
One uses often so-called fully-connected feed-forward neural networks with three or more layers (an input layer, one or more hidden layers and an output layer) consisting of neurons that have non-linear activation functions.
Such networks are often called multilayer perceptrons (MLPs).
According to the Universal approximation theorem, a feed-forward neural network with just a single hidden layer containing a finite number of neurons can approximate a continuous multidimensional function to arbitrary accuracy, assuming the activation function for the hidden layer is a non-constant, bounded and monotonically-increasing continuous function.
Note that the requirements on the activation function only applies to the hidden layer, the output nodes are always assumed to be linear, so as to not restrict the range of output values.
The output \( y \) is produced via the activation function \( f \) $$ y = f\left(\sum_{i=1}^n w_ix_i + b_i\right) = f(z), $$ This function receives \( x_i \) as inputs. Here the activation \( z=(\sum_{i=1}^n w_ix_i+b_i) \). In an FFNN of such neurons, the inputs \( x_i \) are the outputs of the neurons in the preceding layer. Furthermore, an MLP is fully-connected, which means that each neuron receives a weighted sum of the outputs of all neurons in the previous layer.
First, for each node \( i \) in the first hidden layer, we calculate a weighted sum \( z_i^1 \) of the input coordinates \( x_j \), $$ \begin{equation} z_i^1 = \sum_{j=1}^{M} w_{ij}^1 x_j + b_i^1 \label{_auto1} \end{equation} $$
Here \( b_i \) is the so-called bias which is normally needed in case of zero activation weights or inputs. How to fix the biases and the weights will be discussed below. The value of \( z_i^1 \) is the argument to the activation function \( f_i \) of each node \( i \), The variable \( M \) stands for all possible inputs to a given node \( i \) in the first layer. We define the output \( y_i^1 \) of all neurons in layer 1 as $$ \begin{equation} y_i^1 = f(z_i^1) = f\left(\sum_{j=1}^M w_{ij}^1 x_j + b_i^1\right) \label{outputLayer1} \end{equation} $$
where we assume that all nodes in the same layer have identical activation functions, hence the notation \( f \). In general, we could assume in the more general case that different layers have different activation functions. In this case we would identify these functions with a superscript \( l \) for the \( l \)-th layer, $$ \begin{equation} y_i^l = f^l(u_i^l) = f^l\left(\sum_{j=1}^{N_{l-1}} w_{ij}^l y_j^{l-1} + b_i^l\right) \label{generalLayer} \end{equation} $$
where \( N_l \) is the number of nodes in layer \( l \). When the output of all the nodes in the first hidden layer are computed, the values of the subsequent layer can be calculated and so forth until the output is obtained.
The output of neuron \( i \) in layer 2 is thus, $$ \begin{align} y_i^2 &= f^2\left(\sum_{j=1}^N w_{ij}^2 y_j^1 + b_i^2\right) \label{_auto2}\\ &= f^2\left[\sum_{j=1}^N w_{ij}^2f^1\left(\sum_{k=1}^M w_{jk}^1 x_k + b_j^1\right) + b_i^2\right] \label{outputLayer2} \end{align} $$ where we have substituted \( y_k^1 \) with the inputs \( x_k \). Finally, the ANN output reads $$ \begin{align} y_i^3 &= f^3\left(\sum_{j=1}^N w_{ij}^3 y_j^2 + b_i^3\right) \label{_auto3}\\ &= f_3\left[\sum_{j} w_{ij}^3 f^2\left(\sum_{k} w_{jk}^2 f^1\left(\sum_{m} w_{km}^1 x_m + b_k^1\right) + b_j^2\right) + b_1^3\right] \label{_auto4} \end{align} $$
We can generalize this expression to an MLP with \( l \) hidden layers. The complete functional form is, $$ \begin{align} &y^{l+1}_i = f^{l+1}\left[\!\sum_{j=1}^{N_l} w_{ij}^3 f^l\left(\sum_{k=1}^{N_{l-1}}w_{jk}^{l-1}\left(\dots f^1\left(\sum_{n=1}^{N_0} w_{mn}^1 x_n+ b_m^1\right)\dots\right)+b_k^2\right)+b_1^3\right] && \label{completeNN} \end{align} $$
which illustrates a basic property of MLPs: The only independent variables are the input values \( x_n \).
This confirms that an MLP, despite its quite convoluted mathematical form, is nothing more than an analytic function, specifically a mapping of real-valued vectors \( \hat{x} \in \mathbb{R}^n \rightarrow \hat{y} \in \mathbb{R}^m \).
Furthermore, the flexibility and universality of an MLP can be illustrated by realizing that the expression is essentially a nested sum of scaled activation functions of the form $$ \begin{equation} f(x) = c_1 f(c_2 x + c_3) + c_4 \label{_auto5} \end{equation} $$
where the parameters \( c_i \) are weights and biases. By adjusting these parameters, the activation functions can be shifted up and down or left and right, change slope or be rescaled which is the key to the flexibility of a neural network.
We can introduce a more convenient notation for the activations in an A NN.
Additionally, we can represent the biases and activations as layer-wise column vectors \( \hat{b}_l \) and \( \hat{y}_l \), so that the \( i \)-th element of each vector is the bias \( b_i^l \) and activation \( y_i^l \) of node \( i \) in layer \( l \) respectively.
We have that \( \mathrm{W}_l \) is an \( N_{l-1} \times N_l \) matrix, while \( \hat{b}_l \) and \( \hat{y}_l \) are \( N_l \times 1 \) column vectors. With this notation, the sum becomes a matrix-vector multiplication, and we can write the equation for the activations of hidden layer 2 (assuming three nodes for simplicity) as $$ \begin{equation} \hat{y}_2 = f_2(\mathrm{W}_2 \hat{y}_{1} + \hat{b}_{2}) = f_2\left(\left[\begin{array}{ccc} w^2_{11} &w^2_{12} &w^2_{13} \\ w^2_{21} &w^2_{22} &w^2_{23} \\ w^2_{31} &w^2_{32} &w^2_{33} \\ \end{array} \right] \cdot \left[\begin{array}{c} y^1_1 \\ y^1_2 \\ y^1_3 \\ \end{array}\right] + \left[\begin{array}{c} b^2_1 \\ b^2_2 \\ b^2_3 \\ \end{array}\right]\right). \label{_auto6} \end{equation} $$
The activation of node \( i \) in layer 2 is $$ \begin{equation} y^2_i = f_2\Bigr(w^2_{i1}y^1_1 + w^2_{i2}y^1_2 + w^2_{i3}y^1_3 + b^2_i\Bigr) = f_2\left(\sum_{j=1}^3 w^2_{ij} y_j^1 + b^2_i\right). \label{_auto7} \end{equation} $$
This is not just a convenient and compact notation, but also a useful and intuitive way to think about MLPs: The output is calculated by a series of matrix-vector multiplications and vector additions that are used as input to the activation functions. For each operation \( \mathrm{W}_l \hat{y}_{l-1} \) we move forward one layer.
A property that characterizes a neural network, other than its connectivity, is the choice of activation function(s). As described in, the following restrictions are imposed on an activation function for a FFNN to fulfill the universal approximation theorem
The second requirement excludes all linear functions. Furthermore, in a MLP with only linear activation functions, each layer simply performs a linear transformation of its inputs.
Regardless of the number of layers, the output of the NN will be nothing but a linear function of the inputs. Thus we need to introduce some kind of non-linearity to the NN to be able to fit non-linear functions Typical examples are the logistic Sigmoid $$ f(x) = \frac{1}{1 + e^{-x}}, $$ and the hyperbolic tangent function $$ f(x) = \tanh(x) $$
The sigmoid function are more biologically plausible because the output of inactive neurons are zero. Such activation function are called one-sided. However, it has been shown that the hyperbolic tangent performs better than the sigmoid for training MLPs. has become the most popular for deep neural networks
"""The sigmoid function (or the logistic curve) is a
function that takes any real number, z, and outputs a number (0,1).
It is useful in neural networks for assigning weights on a relative scale.
The value z is the weighted sum of parameters involved in the learning algorithm."""
import numpy
import matplotlib.pyplot as plt
import math as mt
z = numpy.arange(-5, 5, .1)
sigma_fn = numpy.vectorize(lambda z: 1/(1+numpy.exp(-z)))
sigma = sigma_fn(z)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(z, sigma)
ax.set_ylim([-0.1, 1.1])
ax.set_xlim([-5,5])
ax.grid(True)
ax.set_xlabel('z')
ax.set_title('sigmoid function')
plt.show()
"""Step Function"""
z = numpy.arange(-5, 5, .02)
step_fn = numpy.vectorize(lambda z: 1.0 if z >= 0.0 else 0.0)
step = step_fn(z)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(z, step)
ax.set_ylim([-0.5, 1.5])
ax.set_xlim([-5,5])
ax.grid(True)
ax.set_xlabel('z')
ax.set_title('step function')
plt.show()
"""Sine Function"""
z = numpy.arange(-2*mt.pi, 2*mt.pi, 0.1)
t = numpy.sin(z)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(z, t)
ax.set_ylim([-1.0, 1.0])
ax.set_xlim([-2*mt.pi,2*mt.pi])
ax.grid(True)
ax.set_xlabel('z')
ax.set_title('sine function')
plt.show()
"""Plots a graph of the squashing function used by a rectified linear
unit"""
z = numpy.arange(-2, 2, .1)
zero = numpy.zeros(len(z))
y = numpy.max([zero, z], axis=0)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(z, y)
ax.set_ylim([-2.0, 2.0])
ax.set_xlim([-2.0, 2.0])
ax.grid(True)
ax.set_xlabel('z')
ax.set_title('Rectified linear unit')
plt.show()
The multilayer perceptron is a very popular, and easy to implement approach, to deep learning. It consists of
For an MLP network there is no direct connection between the output nodes/neurons/units and the input nodes/neurons/units. Hereafter we will call the various entities of a layer for nodes. There are also no connections within a single layer.
The number of input nodes does not need to equal the number of output nodes. This applies also to the hidden layers. Each layer may have its own number of nodes and activation functions.
The hidden layers have their name from the fact that they are not linked to observables and as we will see below when we define the so-called activation \( \hat{z} \), we can think of this as a basis expansion of the original inputs \( \hat{x} \). The difference however between neural networks and say linear regression is that now these basis functions (which will correspond to the weights in the network) are learned from data. This results in an important difference between neural networks and deep learning approaches on one side and methods like logistic regression or linear regression and their modifications on the other side.
A neural network with only one layer, what we called the simple perceptron, is best suited if we have a standard binary model with clear (linear) boundaries between the outcomes. As such it could equally well be replaced by standard linear regression or logistic regression. Networks with one or more hidden layers approximate systems with more complex boundaries.
As stated earlier, an important theorem in studies of neural networks, restated without proof here, is the universal approximation theorem.
It states that a feed-forward network with a single hidden layer containing a finite number of neurons can approximate continuous functions on compact subsets of real functions. The theorem thus states that simple neural networks can represent a wide variety of interesting functions when given appropriate parameters. It is the multilayer feedforward architecture itself which gives neural networks the potential of being universal approximators.
As we have seen now in a feed forward network, we can express the final output of our network in terms of basic matrix-vector multiplications. The unknowwn quantities are our weights \( w_{ij} \) and we need to find an algorithm for changing them so that our errors are as small as possible. This leads us to the famous back propagation algorithm.
The questions we want to ask are how do changes in the biases and the weights in our network change the cost function and how can we use the final output to modify the weights?
To derive these equations let us start with a plain regression problem and define our cost function as $$ {\cal C}(\hat{W}) = \frac{1}{2}\sum_{i=1}^n\left(y_i - t_i\right)^2, $$
where the $t_i$s are our \( n \) targets (the values we want to reproduce), while the outputs of the network after having propagated all inputs \( \hat{x} \) are given by \( y_i \). Below we will demonstrate how the basic equations arising from the back propagation algorithm can be modified in order to study classification problems with \( K \) classes.
With our definition of the targets \( \hat{t} \), the outputs of the network \( \hat{y} \) and the inputs \( \hat{x} \) we define now the activation \( z_j^l \) of node/neuron/unit \( j \) of the \( l \)-th layer as a function of the bias, the weights which add up from the previous layer \( l-1 \) and the forward passes/outputs \( \hat{a}^{l-1} \) from the previous layer as $$ z_j^l = \sum_{i=1}^{M_{l-1}}w_{ij}^la_i^{l-1}+b_j^l, $$
where \( b_k^l \) are the biases from layer \( l \). Here \( M_{l-1} \) represents the total number of nodes/neurons/units of layer \( l-1 \). The figure here illustrates this equation. We can rewrite this in a more compact form as the matrix-vector products we discussed earlier, $$ \hat{z}^l = \left(\hat{W}^l\right)^T\hat{a}^{l-1}+\hat{b}^l. $$
With the activation values \( \hat{z}^l \) we can in turn define the output of layer \( l \) as \( \hat{a}^l = f(\hat{z}^l) \) where \( f \) is our activation function. In the examples here we will use the sigmoid function discussed in our logistic regression lectures. We will also use the same activation function \( f \) for all layers and their nodes. It means we have $$ a_j^l = f(z_j^l) = \frac{1}{1+\exp{-(z_j^l)}}. $$
From the definition of the activation \( z_j^l \) we have $$ \frac{\partial z_j^l}{\partial w_{ij}^l} = a_i^{l-1}, $$ and $$ \frac{\partial z_j^l}{\partial a_i^{l-1}} = w_{ji}^l. $$
With our definition of the activation function we have that (note that this function depends only on \( z_j^l \)) $$ \frac{\partial a_j^l}{\partial z_j^{l}} = a_j^l(1-a_j^l)=f(z_j^l)(1-f(z_j^l)). $$
With these definitions we can now compute the derivative of the cost function in terms of the weights.
Let us specialize to the output layer \( l=L \). Our cost function is $$ {\cal C}(\hat{W^L}) = \frac{1}{2}\sum_{i=1}^n\left(y_i - t_i\right)^2=\frac{1}{2}\sum_{i=1}^n\left(a_i^L - t_i\right)^2, $$ The derivative of this function with respect to the weights is $$ \frac{\partial{\cal C}(\hat{W^L})}{\partial w_{jk}^L} = \left(a_j^L - t_j\right)\frac{\partial a_j^L}{\partial w_{jk}^{L}}, $$ The last partial derivative can easily be computed and reads (by applying the chain rule) $$ \frac{\partial a_j^L}{\partial w_{jk}^{L}} = \frac{\partial a_j^L}{\partial z_{j}^{L}}\frac{\partial z_j^L}{\partial w_{jk}^{L}}=a_j^L(1-a_j^L)a_k^{L-1}, $$
We have thus $$ \frac{\partial{\cal C}(\hat{W^L})}{\partial w_{jk}^L} = \left(a_j^L - t_j\right)a_j^L(1-a_j^L)a_k^{L-1}, $$
Defining $$ \delta_j^L = a_j^L(1-a_j^L)\left(a_j^L - t_j\right) = f'(z_j^L)\frac{\partial {\cal C}}{\partial (a_j^L)}, $$ and using the Hadamard product of two vectors we can write this as $$ \hat{\delta}^L = f'(\hat{z}^L)\circ\frac{\partial {\cal C}}{\partial (\hat{a}^L)}. $$
This is an important expression. The second term on the right handside measures how fast the cost function is changing as a function of the $j$th output activation. If, for example, the cost function doesn't depend much on a particular output node \( j \), then \( \delta_j^L \) will be small, which is what we would expect. The first term on the right, measures how fast the activation function \( f \) is changing at a given activation value \( z_j^L \).
Notice that everything in the above equations is easily computed. In particular, we compute \( z_j^L \) while computing the behaviour of the network, and it is only a small additional overhead to compute \( f'(z^L_j) \). The exact form of the derivative with respect to the output depends on the form of the cost function. However, provided the cost function is known there should be little trouble in calculating $$ \frac{\partial {\cal C}}{\partial (a_j^L)} $$
With the definition of \( \delta_j^L \) we have a more compact definition of the derivative of the cost function in terms of the weights, namely $$ \frac{\partial{\cal C}(\hat{W^L})}{\partial w_{jk}^L} = \delta_j^La_k^{L-1}. $$
It is also easy to see that our previous equation can be written as
$$
\delta_j^L =\frac{\partial {\cal C}}{\partial z_j^L}= \frac{\partial {\cal C}}{\partial a_j^L}\frac{\partial a_j^L}{\partial z_j^L},
$$
which can also be interpreted as the partial derivative of the cost function with respect to the biases \( b_j^L \), namely
$$
\delta_j^L = \frac{\partial {\cal C}}{\partial b_j^L}\frac{\partial b_j^L}{\partial z_j^L}=\frac{\partial {\cal C}}{\partial b_j^L},
$$
That is, the error \( \delta_j^L \) is exactly equal to the rate of change of the cost function as a function of the bias.
We have now three equations that are essential for the computations of the derivatives of the cost function at the output layer. These equations are needed to start the algorithm and they are
$$ \begin{equation} \frac{\partial{\cal C}(\hat{W^L})}{\partial w_{jk}^L} = \delta_j^La_k^{L-1}, \label{_auto8} \end{equation} $$ and $$ \begin{equation} \delta_j^L = f'(z_j^L)\frac{\partial {\cal C}}{\partial (a_j^L)}, \label{_auto9} \end{equation} $$ and $$ \begin{equation} \delta_j^L = \frac{\partial {\cal C}}{\partial b_j^L}, \label{_auto10} \end{equation} $$
An interesting consequence of the above equations is that when the activation \( a_k^{L-1} \) is small, the gradient term, that is the derivative of the cost function with respect to the weights, will also tend to be small. We say then that the weight learns slowly, meaning that it changes slowly when we minimize the weights via say gradient descent. In this case we say the system learns slowly.
Another interesting feature is that is when the activation function, represented by the sigmoid function here, is rather flat when we move towards its end values \( 0 \) and \( 1 \) (see the above Python codes). In these cases, the derivatives of the activation function will also be close to zero, meaning again that the gradients will be small and the network learns slowly again.
We need a fourth equation and we are set. We are going to propagate backwards in order to the determine the weights and biases. In order to do so we need to represent the error in the layer before the final one \( L-1 \) in terms of the errors in the final output layer.
We have that (replacing \( L \) with a general layer \( l \)) $$ \delta_j^l =\frac{\partial {\cal C}}{\partial z_j^l}. $$ We want to express this in terms of the equations for layer \( l+1 \). Using the chain rule and summing over all \( k \) entries we have $$ \delta_j^l =\sum_k \frac{\partial {\cal C}}{\partial z_k^{l+1}}\frac{\partial z_k^{l+1}}{\partial z_j^{l}}=\sum_k \delta_k^{l+1}\frac{\partial z_k^{l+1}}{\partial z_j^{l}}, $$ and recalling that $$ z_j^{l+1} = \sum_{i=1}^{M_{l}}w_{ij}^{l+1}a_i^{l}+b_j^{l+1}, $$ with \( M_l \) being the number of nodes in layer \( l \), we obtain $$ \delta_j^l =\sum_k \delta_k^{l+1}w_{kj}^{l+1}f'(z_j^l), $$ This is our final equation.
We are now ready to set up the algorithm for back propagation and learning the weights and biases.
The four equations provide us with a way of computing the gradient of the cost function. Let us write this out in the form of an algorithm.
First, we set up the input data \( \hat{x} \) and the activations \( \hat{z}_1 \) of the input layer and compute the activation function and the pertinent outputs \( \hat{a}^1 \).
Secondly, we perform then the feed forward till we reach the output layer and compute all \( \hat{z}_l \) of the input layer and compute the activation function and the pertinent outputs \( \hat{a}^l \) for \( l=2,3,\dots,L \).
Thereafter we compute the ouput error \( \hat{\delta}^L \) by computing all $$ \delta_j^L = f'(z_j^L)\frac{\partial {\cal C}}{\partial (a_j^L)}. $$
Then we compute the back propagate error for each \( l=L-1,L-2,\dots,2 \) as $$ \delta_j^l = \sum_k \delta_k^{l+1}w_{kj}^{l+1}f'(z_j^l). $$
Finally, we update the weights and the biases using gradient descent for each \( l=L-1,L-2,\dots,2 \) and update the weights and biases according to the rules $$ w_{jk}^l\leftarrow = w_{jk}^l- \eta \delta_j^la_k^{l-1}, $$ $$ b_j^l \leftarrow b_j^l-\eta \frac{\partial {\cal C}}{\partial b_j^l}=b_j^l-\eta \delta_j^l, $$
The parameter \( \eta \) is the learning parameter discussed in connection with the gradient descent methods. Here it is convenient to use stochastic gradient descent (see the examples below) with mini-batches with an outer loop that steps through multiple epochs of training.
We are now gong to develop an example based on the MNIST data base. This is a classification problem and we need to use our cross-entropy function we discussed in connection with logistic regression. The cross-entropy defines our cost function for the classificaton problems with neural networks.
In binary classification with two classes \( (0, 1) \) we define the logistic/sigmoid function as the probability that a particular input is in class \( 0 \) or \( 1 \). This is possible because the logistic function takes any input from the real numbers and inputs a number between 0 and 1, and can therefore be interpreted as a probability. It also has other nice properties, such as a derivative that is simple to calculate.
For an input \( \boldsymbol{a} \) from the hidden layer, the probability that the input \( \boldsymbol{x} \) is in class 0 or 1 is just. We let \( \theta \) represent the unknown weights and biases to be adjusted by our equations). The variable \( x \) represents our activation values \( z \). We have $$ P(y = 0 \mid \hat{x}, \hat{\theta}) = \frac{1}{1 + \exp{(- \hat{x}})} , $$ and $$ P(y = 1 \mid \hat{x}, \hat{\theta}) = 1 - P(y = 0 \mid \hat{x}, \hat{\theta}) , $$
where \( y \in \{0, 1\} \) and \( \hat{\theta} \) represents the weights and biases of our network.
Our cost function is given as (see the Logistic regression lectures) $$ \mathcal{C}(\hat{\theta}) = - \ln P(\mathcal{D} \mid \hat{\theta}) = - \sum_{i=1}^n y_i \ln[P(y_i = 0)] + (1 - y_i) \ln [1 - P(y_i = 0)] = \sum_{i=1}^n \mathcal{L}_i(\hat{\theta}) . $$
This last equality means that we can interpret our cost function as a sum over the loss function for each point in the dataset \( \mathcal{L}_i(\hat{\theta}) \). The negative sign is just so that we can think about our algorithm as minimizing a positive number, rather than maximizing a negative number.
In multiclass classification it is common to treat each integer label as a so called one-hot vector:
\( y = 5 \quad \rightarrow \quad \hat{y} = (0, 0, 0, 0, 0, 1, 0, 0, 0, 0) , \) and
\( y = 1 \quad \rightarrow \quad \hat{y} = (0, 1, 0, 0, 0, 0, 0, 0, 0, 0) , \)
i.e. a binary bit string of length \( C \), where \( C = 10 \) is the number of classes in the MNIST dataset (numbers from \( 0 \) to \( 9 \))..
If \( \hat{x}_i \) is the \( i \)-th input (image), \( y_{ic} \) refers to the \( c \)-th component of the \( i \)-th output vector \( \hat{y}_i \). The probability of \( \hat{x}_i \) being in class \( c \) will be given by the softmax function: $$ P(y_{ic} = 1 \mid \hat{x}_i, \hat{\theta}) = \frac{\exp{((\hat{a}_i^{hidden})^T \hat{w}_c)}} {\sum_{c'=0}^{C-1} \exp{((\hat{a}_i^{hidden})^T \hat{w}_{c'})}} , $$
which reduces to the logistic function in the binary case. The likelihood of this \( C \)-class classifier is now given as: $$ P(\mathcal{D} \mid \hat{\theta}) = \prod_{i=1}^n \prod_{c=0}^{C-1} [P(y_{ic} = 1)]^{y_{ic}} . $$ Again we take the negative log-likelihood to define our cost function: $$ \mathcal{C}(\hat{\theta}) = - \log{P(\mathcal{D} \mid \hat{\theta})}. $$ See the logistic regression lectures for a full definition of the cost function.
The back propagation equations need now only a small change, namely the definition of a new cost function. We are thus ready to use the same equations as before!
As an example of the above, relevant for project 2 as well, let us consider a binary class. As discussed in our logistic regression lectures, we defined a cost function in terms of the parameters \( \beta \) as $$ \mathcal{C}(\hat{\beta}) = - \sum_{i=1}^n \left(y_i\log{p(y_i \vert x_i,\hat{\beta})}+(1-y_i)\log{1-p(y_i \vert x_i,\hat{\beta})}\right), $$ where we had defined the logistic (sigmoid) function $$ p(y_i =1\vert x_i,\hat{\beta})=\frac{\exp{(\beta_0+\beta_1 x_i)}}{1+\exp{(\beta_0+\beta_1 x_i)}}, $$ and $$ p(y_i =0\vert x_i,\hat{\beta})=1-p(y_i =1\vert x_i,\hat{\beta}). $$ The parameters \( \hat{\beta} \) were defined using a minimization method like gradient descent or Newton-Raphson's method.
Now we replace \( x_i \) with the activation \( z_i^l \) for a given layer \( l \) and the outputs as \( y_i=a_i^l=f(z_i^l) \), with \( z_i^l \) now being a function of the weights \( w_{ij}^l \) and biases \( b_i^l \). We have then $$ a_i^l = y_i = \frac{\exp{(z_i^l)}}{1+\exp{(z_i^l)}}, $$ with $$ z_i^l = \sum_{j}w_{ij}^l a_j^{l-1}+b_i^l, $$ where the superscript \( l-1 \) indicates that these are the outputs from layer \( l-1 \). Our cost function at the final layer \( l=L \) is now $$ \mathcal{C}(\hat{W}) = - \sum_{i=1}^n \left(t_i\log{a_i^L}+(1-t_i)\log{(1-a_i^L)}\right), $$ where we have defined the targets \( t_i \). The derivatives of the cost function with respect to the output \( a_i^L \) are then easily calculated and we get $$ \frac{\partial \mathcal{C}(\hat{W})}{\partial a_i^L} = \frac{a_i^L-t_i}{a_i^L(1-a_i^L)}. $$ In case we use another activation function than the logistic one, we need to evaluate other derivatives.
In case we employ the more general case given by the Softmax equation, we need to evaluate the derivative of the activation function with respect to the activation \( z_i^l \), that is we need $$ \frac{\partial f(z_i^l)}{\partial w_{jk}^l} = \frac{\partial f(z_i^l)}{\partial z_j^l} \frac{\partial z_j^l}{\partial w_{jk}^l}= \frac{\partial f(z_i^l)}{\partial z_j^l}a_k^{l-1}. $$ For the Softmax function we have $$ f(z_i^l) = \frac{\exp{(z_i^l)}}{\sum_{m=1}^K\exp{(z_m^l)}}. $$ Its derivative with respect to \( z_j^l \) gives $$ \frac{\partial f(z_i^l)}{\partial z_j^l}= f(z_i^l)\left(\delta_{ij}-f(z_j^l)\right), $$ which in case of the simply binary model reduces to having \( i=j \).
One can identify a set of key steps when using neural networks to solve supervised learning problems:
Here we will be using the MNIST dataset, which is readily available through the scikit-learn package. You may also find it for example here. The MNIST (Modified National Institute of Standards and Technology) database is a large database of handwritten digits that is commonly used for training various image processing systems. The MNIST dataset consists of 70 000 images of size \( 28\times 28 \) pixels, each labeled from 0 to 9. The scikit-learn dataset we will use consists of a selection of 1797 images of size \( 8\times 8 \) collected and processed from this database.
To feed data into a feed-forward neural network we need to represent the inputs as a design/feature matrix \( X = (n_{inputs}, n_{features}) \). Each row represents an input, in this case a handwritten digit, and each column represents a feature, in this case a pixel. The correct answers, also known as labels or targets are represented as a 1D array of integers \( Y = (n_{inputs}) = (5, 3, 1, 8,...) \).
As an example, say we want to build a neural network using supervised learning to predict Body-Mass Index (BMI) from measurements of height (in m) and weight (in kg). If we have measurements of 5 people the design/feature matrix could be for example: $$ X = \begin{bmatrix} 1.85 & 81\\ 1.71 & 65\\ 1.95 & 103\\ 1.55 & 42\\ 1.63 & 56 \end{bmatrix} ,$$
and the targets would be: $$ Y = (23.7, 22.2, 27.1, 17.5, 21.1) $$
Since each input image is a 2D matrix, we need to flatten the image (i.e. "unravel" the 2D matrix into a 1D array) to turn the data into a design/feature matrix. This means we lose all spatial information in the image, such as locality and translational invariance. More complicated architectures such as Convolutional Neural Networks can take advantage of such information, and are most commonly applied when analyzing images.
# import necessary packages
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
# ensure the same random numbers appear every time
np.random.seed(0)
# display images in notebook
%matplotlib inline
plt.rcParams['figure.figsize'] = (12,12)
# download MNIST dataset
digits = datasets.load_digits()
# define inputs and labels
inputs = digits.images
labels = digits.target
print("inputs = (n_inputs, pixel_width, pixel_height) = " + str(inputs.shape))
print("labels = (n_inputs) = " + str(labels.shape))
# flatten the image
# the value -1 means dimension is inferred from the remaining dimensions: 8x8 = 64
n_inputs = len(inputs)
inputs = inputs.reshape(n_inputs, -1)
print("X = (n_inputs, n_features) = " + str(inputs.shape))
# choose some random images to display
indices = np.arange(n_inputs)
random_indices = np.random.choice(indices, size=5)
for i, image in enumerate(digits.images[random_indices]):
plt.subplot(1, 5, i+1)
plt.axis('off')
plt.imshow(image, cmap=plt.cm.gray_r, interpolation='nearest')
plt.title("Label: %d" % digits.target[random_indices[i]])
plt.show()
Performing analysis before partitioning the dataset is a major error, that can lead to incorrect conclusions.
We will reserve \( 80 \% \) of our dataset for training and \( 20 \% \) for testing.
It is important that the train and test datasets are drawn randomly from our dataset, to ensure no bias in the sampling. Say you are taking measurements of weather data to predict the weather in the coming 5 days. You don't want to train your model on measurements taken from the hours 00.00 to 12.00, and then test it on data collected from 12.00 to 24.00.
from sklearn.model_selection import train_test_split
# one-liner from scikit-learn library
train_size = 0.8
test_size = 1 - train_size
X_train, X_test, Y_train, Y_test = train_test_split(inputs, labels, train_size=train_size,
test_size=test_size)
# equivalently in numpy
def train_test_split_numpy(inputs, labels, train_size, test_size):
n_inputs = len(inputs)
inputs_shuffled = inputs.copy()
labels_shuffled = labels.copy()
np.random.shuffle(inputs_shuffled)
np.random.shuffle(labels_shuffled)
train_end = int(n_inputs*train_size)
X_train, X_test = inputs_shuffled[:train_end], inputs_shuffled[train_end:]
Y_train, Y_test = labels_shuffled[:train_end], labels_shuffled[train_end:]
return X_train, X_test, Y_train, Y_test
#X_train, X_test, Y_train, Y_test = train_test_split_numpy(inputs, labels, train_size, test_size)
print("Number of training images: " + str(len(X_train)))
print("Number of test images: " + str(len(X_test)))
Our simple feed-forward neural network will consist of an input layer, a single hidden layer and an output layer. The activation \( y \) of each neuron is a weighted sum of inputs, passed through an activation function. In case of the simple perceptron model we have $$ z = \sum_{i=1}^n w_i a_i ,$$ $$ y = f(z) ,$$
where \( f \) is the activation function, \( a_i \) represents input from neuron \( i \) in the preceding layer and \( w_i \) is the weight to input \( i \). The activation of the neurons in the input layer is just the features (e.g. a pixel value).
The simplest activation function for a neuron is the Heaviside function: $$ f(z) = \begin{cases} 1, & z > 0\\ 0, & \text{otherwise} \end{cases} $$
A feed-forward neural network with this activation is known as a perceptron. For a binary classifier (i.e. two classes, 0 or 1, dog or not-dog) we can also use this in our output layer. This activation can be generalized to \( k \) classes (using e.g. the one-against-all strategy), and we call these architectures multiclass perceptrons.
However, it is now common to use the terms Single Layer Perceptron (SLP) (1 hidden layer) and Multilayer Perceptron (MLP) (2 or more hidden layers) to refer to feed-forward neural networks with any activation function.
Typical choices for activation functions include the sigmoid function, hyperbolic tangent, and Rectified Linear Unit (ReLU). We will be using the sigmoid function \( \sigma(x) \): $$ f(x) = \sigma(x) = \frac{1}{1 + e^{-x}} ,$$
which is inspired by probability theory (see logistic regression) and was most commonly used until about 2011. See the discussion below concerning other activation functions.
For a soft binary classifier, we could use a single neuron and interpret the output as either being the probability of being in class 0 or the probability of being in class 1. Alternatively we could use 2 neurons, and interpret each neuron as the probability of being in each class.
Since we are doing multiclass classification, with 10 categories, it is natural to use 10 neurons in the output layer. We number the neurons \( j = 0,1,...,9 \). The activation of each output neuron \( j \) will be according to the softmax function: $$ P(\text{class \( j \)} \mid \text{input \( \hat{a} \)}) = \frac{\exp{(\hat{a}^T \hat{w}_j)}} {\sum_{c=0}^{9} \exp{(\hat{a}^T \hat{w}_c)}} ,$$
i.e. each neuron \( j \) outputs the probability of being in class \( j \) given an input from the hidden layer \( \hat{a} \), with \( \hat{w}_j \) the weights of neuron \( j \) to the inputs. The denominator is a normalization factor to ensure the outputs (probabilities) sum up to 1. The exponent is just the weighted sum of inputs as before: $$ z_j = \sum_{i=1}^n w_ {ij} a_i+b_j.$$
Since each neuron in the output layer is connected to the 50 inputs from the hidden layer we have 50x10 = 500 weights to the output layer.
Typically weights are initialized with small values distributed around zero, drawn from a uniform or normal distribution. Setting all weights to zero means all neurons give the same output, making the network useless.
Adding a bias value to the weighted sum of inputs allows the neural network to represent a greater range of values. Without it, any input with the value 0 will be mapped to zero (before being passed through the activation). The bias unit has an output of 1, and a weight to each neuron \( j \), \( b_j \): $$ z_j = \sum_{i=1}^n w_ {ij} a_i + b_j.$$
The bias weights \( \hat{b} \) are often initialized to zero, but a small value like \( 0.01 \) ensures all neurons have some output which can be backpropagated in the first training cycle.
# building our neural network
n_inputs, n_features = X_train.shape
n_hidden_neurons = 50
n_categories = 10
# we make the weights normally distributed using numpy.random.randn
# weights and bias in the hidden layer
hidden_weights = np.random.randn(n_features, n_hidden_neurons)
hidden_bias = np.zeros(n_hidden_neurons) + 0.01
# weights and bias in the output layer
output_weights = np.random.randn(n_hidden_neurons, n_categories)
output_bias = np.zeros(n_categories) + 0.01
Denote \( F \) the number of features, \( H \) the number of hidden neurons and \( C \) the number of categories. For each input image we calculate a weighted sum of input features (pixel values) to each neuron \( j \) in the hidden layer \( l \): $$ z_{j}^{l} = \sum_{i=1}^{F} w_{ij}^{l} x_i + b_{j}^{l},$$
this is then passed through our activation function $$ a_{j}^{l} = f(z_{j}^{l}) .$$
We calculate a weighted sum of inputs (activations in the hidden layer) to each neuron \( j \) in the output layer: $$ z_{j}^{L} = \sum_{i=1}^{H} w_{ij}^{L} a_{i}^{l} + b_{j}^{L}.$$
Finally we calculate the output of neuron \( j \) in the output layer using the softmax function: $$ a_{j}^{L} = \frac{\exp{(z_j^{L})}} {\sum_{c=0}^{C-1} \exp{(z_c^{L})}} .$$
Since our data has the dimensions \( X = (n_{inputs}, n_{features}) \) and our weights to the hidden layer have the dimensions \( W_{hidden} = (n_{features}, n_{hidden}) \), we can easily feed the network all our training data in one go by taking the matrix product $$ X W^{h} = (n_{inputs}, n_{hidden}),$$
and obtain a matrix that holds the weighted sum of inputs to the hidden layer for each input image and each hidden neuron. We also add the bias to obtain a matrix of weighted sums to the hidden layer \( Z^{h} \): $$ \hat{z}^{l} = \hat{X} \hat{W}^{l} + \hat{b}^{l} ,$$
meaning the same bias (1D array with size equal number of hidden neurons) is added to each input image. This is then passed through the activation: $$ \hat{a}^{l} = f(\hat{z}^l) .$$
This is fed to the output layer: $$ \hat{z}^{L} = \hat{a}^{L} \hat{W}^{L} + \hat{b}^{L} .$$
Finally we receive our output values for each image and each category by passing it through the softmax function: $$ output = softmax (\hat{z}^{L}) = (n_{inputs}, n_{categories}) .$$
# setup the feed-forward pass, subscript h = hidden layer
def sigmoid(x):
return 1/(1 + np.exp(-x))
def feed_forward(X):
# weighted sum of inputs to the hidden layer
z_h = np.matmul(X, hidden_weights) + hidden_bias
# activation in the hidden layer
a_h = sigmoid(z_h)
# weighted sum of inputs to the output layer
z_o = np.matmul(a_h, output_weights) + output_bias
# softmax output
# axis 0 holds each input and axis 1 the probabilities of each category
exp_term = np.exp(z_o)
probabilities = exp_term / np.sum(exp_term, axis=1, keepdims=True)
return probabilities
probabilities = feed_forward(X_train)
print("probabilities = (n_inputs, n_categories) = " + str(probabilities.shape))
print("probability that image 0 is in category 0,1,2,...,9 = \n" + str(probabilities[0]))
print("probabilities sum up to: " + str(probabilities[0].sum()))
print()
# we obtain a prediction by taking the class with the highest likelihood
def predict(X):
probabilities = feed_forward(X)
return np.argmax(probabilities, axis=1)
predictions = predict(X_train)
print("predictions = (n_inputs) = " + str(predictions.shape))
print("prediction for image 0: " + str(predictions[0]))
print("correct label for image 0: " + str(Y_train[0]))
To measure how well our neural network is doing we need to introduce a cost function. We will call the function that gives the error of a single sample output the loss function, and the function that gives the total error of our network across all samples the cost function. A typical choice for multiclass classification is the cross-entropy loss, also known as the negative log likelihood.
In multiclass classification it is common to treat each integer label as a so called one-hot vector: $$ y = 5 \quad \rightarrow \quad \hat{y} = (0, 0, 0, 0, 0, 1, 0, 0, 0, 0) ,$$ $$ y = 1 \quad \rightarrow \quad \hat{y} = (0, 1, 0, 0, 0, 0, 0, 0, 0, 0) ,$$
i.e. a binary bit string of length \( C \), where \( C = 10 \) is the number of classes in the MNIST dataset.
Let \( y_{ic} \) denote the \( c \)-th component of the \( i \)-th one-hot vector. We define the cost function \( \mathcal{C} \) as a sum over the cross-entropy loss for each point \( \hat{x}_i \) in the dataset.
In the one-hot representation only one of the terms in the loss function is non-zero, namely the probability of the correct category \( c' \) (i.e. the category \( c' \) such that \( y_{ic'} = 1 \)). This means that the cross entropy loss only punishes you for how wrong you got the correct label. The probability of category \( c \) is given by the softmax function. The vector \( \hat{\theta} \) represents the parameters of our network, i.e. all the weights and biases.
The network is trained by finding the weights and biases that minimize the cost function. One of the most widely used classes of methods is gradient descent and its generalizations. The idea behind gradient descent is simply to adjust the weights in the direction where the gradient of the cost function is large and negative. This ensures we flow toward a local minimum of the cost function. Each parameter \( \theta \) is iteratively adjusted according to the rule $$ \theta_{i+1} = \theta_i - \eta \nabla \mathcal{C}(\theta_i) ,$$
where \( \eta \) is known as the learning rate, which controls how big a step we take towards the minimum. This update can be repeated for any number of iterations, or until we are satisfied with the result.
A simple and effective improvement is a variant called Batch Gradient Descent. Instead of calculating the gradient on the whole dataset, we calculate an approximation of the gradient on a subset of the data called a minibatch. If there are \( N \) data points and we have a minibatch size of \( M \), the total number of batches is \( N/M \). We denote each minibatch \( B_k \), with \( k = 1, 2,...,N/M \). The gradient then becomes: $$ \nabla \mathcal{C}(\theta) = \frac{1}{N} \sum_{i=1}^N \nabla \mathcal{L}_i(\theta) \quad \rightarrow \quad \frac{1}{M} \sum_{i \in B_k} \nabla \mathcal{L}_i(\theta) ,$$
i.e. instead of averaging the loss over the entire dataset, we average over a minibatch.
This has two important benefits:
It is common to add an extra term to the cost function, proportional to the size of the weights. This is equivalent to constraining the size of the weights, so that they do not grow out of control. Constraining the size of the weights means that the weights cannot grow arbitrarily large to fit the training data, and in this way reduces overfitting.
We will measure the size of the weights using the so called L2-norm, meaning our cost function becomes: $$ \mathcal{C}(\theta) = \frac{1}{N} \sum_{i=1}^N \mathcal{L}_i(\theta) \quad \rightarrow \quad \frac{1}{N} \sum_{i=1}^N \mathcal{L}_i(\theta) + \lambda \lvert \lvert \hat{w} \rvert \rvert_2^2 = \frac{1}{N} \sum_{i=1}^N \mathcal{L}(\theta) + \lambda \sum_{ij} w_{ij}^2,$$
i.e. we sum up all the weights squared. The factor \( \lambda \) is known as a regularization parameter.
In order to train the model, we need to calculate the derivative of the cost function with respect to every bias and weight in the network. In total our network has \( (64 + 1)\times 50=3250 \) weights in the hidden layer and \( (50 + 1)\times 10=510 \) weights to the output layer (\( +1 \) for the bias), and the gradient must be calculated for every parameter. We use the backpropagation algorithm discussed above. This is a clever use of the chain rule that allows us to calculate the gradient efficently.
To more efficently train our network these equations are implemented using matrix operations. The error in the output layer is calculated simply as, with \( \hat{t} \) being our targets, $$ \delta_L = \hat{t} - \hat{y} = (n_{inputs}, n_{categories}) .$$
The gradient for the output weights is calculated as $$ \nabla W_{L} = \hat{a}^T \delta_L = (n_{hidden}, n_{categories}) ,$$
where \( \hat{a} = (n_{inputs}, n_{hidden}) \). This simply means that we are summing up the gradients for each input. Since we are going backwards we have to transpose the activation matrix.
The gradient with respect to the output bias is then $$ \nabla \hat{b}_{L} = \sum_{i=1}^{n_{inputs}} \delta_L = (n_{categories}) .$$
The error in the hidden layer is $$ \Delta_h = \delta_L W_{L}^T \circ f'(z_{h}) = \delta_L W_{L}^T \circ a_{h} \circ (1 - a_{h}) = (n_{inputs}, n_{hidden}) ,$$
where \( f'(a_{h}) \) is the derivative of the activation in the hidden layer. The matrix products mean that we are summing up the products for each neuron in the output layer. The symbol \( \circ \) denotes the Hadamard product, meaning element-wise multiplication.
This again gives us the gradients in the hidden layer: $$ \nabla W_{h} = X^T \delta_h = (n_{features}, n_{hidden}) ,$$ $$ \nabla b_{h} = \sum_{i=1}^{n_{inputs}} \delta_h = (n_{hidden}) .$$
# to categorical turns our integer vector into a onehot representation
from sklearn.metrics import accuracy_score
# one-hot in numpy
def to_categorical_numpy(integer_vector):
n_inputs = len(integer_vector)
n_categories = np.max(integer_vector) + 1
onehot_vector = np.zeros((n_inputs, n_categories))
onehot_vector[range(n_inputs), integer_vector] = 1
return onehot_vector
#Y_train_onehot, Y_test_onehot = to_categorical(Y_train), to_categorical(Y_test)
Y_train_onehot, Y_test_onehot = to_categorical_numpy(Y_train), to_categorical_numpy(Y_test)
def feed_forward_train(X):
# weighted sum of inputs to the hidden layer
z_h = np.matmul(X, hidden_weights) + hidden_bias
# activation in the hidden layer
a_h = sigmoid(z_h)
# weighted sum of inputs to the output layer
z_o = np.matmul(a_h, output_weights) + output_bias
# softmax output
# axis 0 holds each input and axis 1 the probabilities of each category
exp_term = np.exp(z_o)
probabilities = exp_term / np.sum(exp_term, axis=1, keepdims=True)
# for backpropagation need activations in hidden and output layers
return a_h, probabilities
def backpropagation(X, Y):
a_h, probabilities = feed_forward_train(X)
# error in the output layer
error_output = probabilities - Y
# error in the hidden layer
error_hidden = np.matmul(error_output, output_weights.T) * a_h * (1 - a_h)
# gradients for the output layer
output_weights_gradient = np.matmul(a_h.T, error_output)
output_bias_gradient = np.sum(error_output, axis=0)
# gradient for the hidden layer
hidden_weights_gradient = np.matmul(X.T, error_hidden)
hidden_bias_gradient = np.sum(error_hidden, axis=0)
return output_weights_gradient, output_bias_gradient, hidden_weights_gradient, hidden_bias_gradient
print("Old accuracy on training data: " + str(accuracy_score(predict(X_train), Y_train)))
eta = 0.01
lmbd = 0.01
for i in range(1000):
# calculate gradients
dWo, dBo, dWh, dBh = backpropagation(X_train, Y_train_onehot)
# regularization term gradients
dWo += lmbd * output_weights
dWh += lmbd * hidden_weights
# update weights and biases
output_weights -= eta * dWo
output_bias -= eta * dBo
hidden_weights -= eta * dWh
hidden_bias -= eta * dBh
print("New accuracy on training data: " + str(accuracy_score(predict(X_train), Y_train)))
As we can see the network does not seem to be learning at all. It seems to be just guessing the label for each image. In order to obtain a network that does something useful, we will have to do a bit more work.
The choice of hyperparameters such as learning rate and regularization parameter is hugely influential for the performance of the network. Typically a grid-search is performed, wherein we test different hyperparameters separated by orders of magnitude. For example we could test the learning rates \( \eta = 10^{-6}, 10^{-5},...,10^{-1} \) with different regularization parameters \( \lambda = 10^{-6},...,10^{-0} \).
Next, we haven't implemented minibatching yet, which introduces stochasticity and is though to act as an important regularizer on the weights. We call a feed-forward + backward pass with a minibatch an iteration, and a full training period going through the entire dataset (\( n/M \) batches) an epoch.
If this does not improve network performance, you may want to consider altering the network architecture, adding more neurons or hidden layers. Andrew Ng goes through some of these considerations in this video. You can find a summary of the video here.
It is very natural to think of the network as an object, with specific instances of the network being realizations of this object with different hyperparameters. An implementation using Python classes provides a clean structure and interface, and the full implementation of our neural network is given below.
class NeuralNetwork:
def __init__(
self,
X_data,
Y_data,
n_hidden_neurons=50,
n_categories=10,
epochs=10,
batch_size=100,
eta=0.1,
lmbd=0.0):
self.X_data_full = X_data
self.Y_data_full = Y_data
self.n_inputs = X_data.shape[0]
self.n_features = X_data.shape[1]
self.n_hidden_neurons = n_hidden_neurons
self.n_categories = n_categories
self.epochs = epochs
self.batch_size = batch_size
self.iterations = self.n_inputs // self.batch_size
self.eta = eta
self.lmbd = lmbd
self.create_biases_and_weights()
def create_biases_and_weights(self):
self.hidden_weights = np.random.randn(self.n_features, self.n_hidden_neurons)
self.hidden_bias = np.zeros(self.n_hidden_neurons) + 0.01
self.output_weights = np.random.randn(self.n_hidden_neurons, self.n_categories)
self.output_bias = np.zeros(self.n_categories) + 0.01
def feed_forward(self):
# feed-forward for training
self.z_h = np.matmul(self.X_data, self.hidden_weights) + self.hidden_bias
self.a_h = sigmoid(self.z_h)
self.z_o = np.matmul(self.a_h, self.output_weights) + self.output_bias
exp_term = np.exp(self.z_o)
self.probabilities = exp_term / np.sum(exp_term, axis=1, keepdims=True)
def feed_forward_out(self, X):
# feed-forward for output
z_h = np.matmul(X, self.hidden_weights) + self.hidden_bias
a_h = sigmoid(z_h)
z_o = np.matmul(a_h, self.output_weights) + self.output_bias
exp_term = np.exp(z_o)
probabilities = exp_term / np.sum(exp_term, axis=1, keepdims=True)
return probabilities
def backpropagation(self):
error_output = self.probabilities - self.Y_data
error_hidden = np.matmul(error_output, self.output_weights.T) * self.a_h * (1 - self.a_h)
self.output_weights_gradient = np.matmul(self.a_h.T, error_output)
self.output_bias_gradient = np.sum(error_output, axis=0)
self.hidden_weights_gradient = np.matmul(self.X_data.T, error_hidden)
self.hidden_bias_gradient = np.sum(error_hidden, axis=0)
if self.lmbd > 0.0:
self.output_weights_gradient += self.lmbd * self.output_weights
self.hidden_weights_gradient += self.lmbd * self.hidden_weights
self.output_weights -= self.eta * self.output_weights_gradient
self.output_bias -= self.eta * self.output_bias_gradient
self.hidden_weights -= self.eta * self.hidden_weights_gradient
self.hidden_bias -= self.eta * self.hidden_bias_gradient
def predict(self, X):
probabilities = self.feed_forward_out(X)
return np.argmax(probabilities, axis=1)
def predict_probabilities(self, X):
probabilities = self.feed_forward_out(X)
return probabilities
def train(self):
data_indices = np.arange(self.n_inputs)
for i in range(self.epochs):
for j in range(self.iterations):
# pick datapoints with replacement
chosen_datapoints = np.random.choice(
data_indices, size=self.batch_size, replace=False
)
# minibatch training data
self.X_data = self.X_data_full[chosen_datapoints]
self.Y_data = self.Y_data_full[chosen_datapoints]
self.feed_forward()
self.backpropagation()
To measure the performance of our network we evaluate how well it does it data it has never seen before, i.e. the test data. We measure the performance of the network using the accuracy score. The accuracy is as you would expect just the number of images correctly labeled divided by the total number of images. A perfect classifier will have an accuracy score of \( 1 \). $$ \text{Accuracy} = \frac{\sum_{i=1}^n I(\hat{y}_i = y_i)}{n} ,$$
where \( I \) is the indicator function, \( 1 \) if \( \hat{y}_i = y_i \) and \( 0 \) otherwise.
epochs = 100
batch_size = 100
dnn = NeuralNetwork(X_train, Y_train_onehot, eta=eta, lmbd=lmbd, epochs=epochs, batch_size=batch_size,
n_hidden_neurons=n_hidden_neurons, n_categories=n_categories)
dnn.train()
test_predict = dnn.predict(X_test)
# accuracy score from scikit library
print("Accuracy score on test set: ", accuracy_score(Y_test, test_predict))
# equivalent in numpy
def accuracy_score_numpy(Y_test, Y_pred):
return np.sum(Y_test == Y_pred) / len(Y_test)
#print("Accuracy score on test set: ", accuracy_score_numpy(Y_test, test_predict))
We now perform a grid search to find the optimal hyperparameters for the network. Note that we are only using 1 layer with 50 neurons, and human performance is estimated to be around \( 98\% \) (\( 2\% \) error rate).
eta_vals = np.logspace(-5, 1, 7)
lmbd_vals = np.logspace(-5, 1, 7)
# store the models for later use
DNN_numpy = np.zeros((len(eta_vals), len(lmbd_vals)), dtype=object)
# grid search
for i, eta in enumerate(eta_vals):
for j, lmbd in enumerate(lmbd_vals):
dnn = NeuralNetwork(X_train, Y_train_onehot, eta=eta, lmbd=lmbd, epochs=epochs, batch_size=batch_size,
n_hidden_neurons=n_hidden_neurons, n_categories=n_categories)
dnn.train()
DNN_numpy[i][j] = dnn
test_predict = dnn.predict(X_test)
print("Learning rate = ", eta)
print("Lambda = ", lmbd)
print("Accuracy score on test set: ", accuracy_score(Y_test, test_predict))
print()
# visual representation of grid search
# uses seaborn heatmap, you can also do this with matplotlib imshow
import seaborn as sns
sns.set()
train_accuracy = np.zeros((len(eta_vals), len(lmbd_vals)))
test_accuracy = np.zeros((len(eta_vals), len(lmbd_vals)))
for i in range(len(eta_vals)):
for j in range(len(lmbd_vals)):
dnn = DNN_numpy[i][j]
train_pred = dnn.predict(X_train)
test_pred = dnn.predict(X_test)
train_accuracy[i][j] = accuracy_score(Y_train, train_pred)
test_accuracy[i][j] = accuracy_score(Y_test, test_pred)
fig, ax = plt.subplots(figsize = (10, 10))
sns.heatmap(train_accuracy, annot=True, ax=ax, cmap="viridis")
ax.set_title("Training Accuracy")
ax.set_ylabel("$\eta$")
ax.set_xlabel("$\lambda$")
plt.show()
fig, ax = plt.subplots(figsize = (10, 10))
sns.heatmap(test_accuracy, annot=True, ax=ax, cmap="viridis")
ax.set_title("Test Accuracy")
ax.set_ylabel("$\eta$")
ax.set_xlabel("$\lambda$")
plt.show()
scikit-learn focuses more on traditional machine learning methods, such as regression, clustering, decision trees, etc. As such, it has only two types of neural networks: Multi Layer Perceptron outputting continuous values, MPLRegressor, and Multi Layer Perceptron outputting labels, MLPClassifier. We will see how simple it is to use these classes.
scikit-learn implements a few improvements from our neural network, such as early stopping, a varying learning rate, different optimization methods, etc. We would therefore expect a better performance overall.
from sklearn.neural_network import MLPClassifier
# store models for later use
DNN_scikit = np.zeros((len(eta_vals), len(lmbd_vals)), dtype=object)
for i, eta in enumerate(eta_vals):
for j, lmbd in enumerate(lmbd_vals):
dnn = MLPClassifier(hidden_layer_sizes=(n_hidden_neurons), activation='logistic',
alpha=lmbd, learning_rate_init=eta, max_iter=epochs)
dnn.fit(X_train, Y_train)
DNN_scikit[i][j] = dnn
print("Learning rate = ", eta)
print("Lambda = ", lmbd)
print("Accuracy score on test set: ", dnn.score(X_test, Y_test))
print()
# optional
# visual representation of grid search
# uses seaborn heatmap, could probably do this in matplotlib
import seaborn as sns
sns.set()
train_accuracy = np.zeros((len(eta_vals), len(lmbd_vals)))
test_accuracy = np.zeros((len(eta_vals), len(lmbd_vals)))
for i in range(len(eta_vals)):
for j in range(len(lmbd_vals)):
dnn = DNN_scikit[i][j]
train_pred = dnn.predict(X_train)
test_pred = dnn.predict(X_test)
train_accuracy[i][j] = accuracy_score(Y_train, train_pred)
test_accuracy[i][j] = accuracy_score(Y_test, test_pred)
fig, ax = plt.subplots(figsize = (10, 10))
sns.heatmap(train_accuracy, annot=True, ax=ax, cmap="viridis")
ax.set_title("Training Accuracy")
ax.set_ylabel("$\eta$")
ax.set_xlabel("$\lambda$")
plt.show()
fig, ax = plt.subplots(figsize = (10, 10))
sns.heatmap(test_accuracy, annot=True, ax=ax, cmap="viridis")
ax.set_title("Test Accuracy")
ax.set_ylabel("$\eta$")
ax.set_xlabel("$\lambda$")
plt.show()
Now we want to build on the experience gained from our neural network implementation in NumPy and scikit-learn and use it to construct a neural network in Tensorflow. Once we have constructed a neural network in NumPy and Tensorflow, building one in Keras is really quite trivial, though the performance may suffer.
In our previous example we used only one hidden layer, and in this we will use two. From this it should be quite clear how to build one using an arbitrary number of hidden layers, using data structures such as Python lists or NumPy arrays.
Tensorflow is an open source library machine learning library developed by the Google Brain team for internal use. It was released under the Apache 2.0 open source license in November 9, 2015.
Tensorflow is a computational framework that allows you to construct machine learning models at different levels of abstraction, from high-level, object-oriented APIs like Keras, down to the C++ kernels that Tensorflow is built upon. The higher levels of abstraction are simpler to use, but less flexible, and our choice of implementation should reflect the problems we are trying to solve.
Tensorflow uses so-called graphs to represent your computation in terms of the dependencies between individual operations, such that you first build a Tensorflow graph to represent your model, and then create a Tensorflow session to run the graph.
In this guide we will analyze the same data as we did in our NumPy and scikit-learn tutorial, gathered from the MNIST database of images. We will give an introduction to the lower level Python Application Program Interfaces (APIs), and see how we use them to build our graph. Then we will build (effectively) the same graph in Keras, to see just how simple solving a machine learning problem can be.
To install tensorflow on Unix/Linux systems, use pip as
pip install tensorflow
and/or if you use anaconda, just write (or install from the graphical user interface)
conda install tensorflow
# import necessary packages
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
# ensure the same random numbers appear every time
np.random.seed(0)
# display images in notebook
%matplotlib inline
plt.rcParams['figure.figsize'] = (12,12)
# download MNIST dataset
digits = datasets.load_digits()
# define inputs and labels
inputs = digits.images
labels = digits.target
print("inputs = (n_inputs, pixel_width, pixel_height) = " + str(inputs.shape))
print("labels = (n_inputs) = " + str(labels.shape))
# flatten the image
# the value -1 means dimension is inferred from the remaining dimensions: 8x8 = 64
n_inputs = len(inputs)
inputs = inputs.reshape(n_inputs, -1)
print("X = (n_inputs, n_features) = " + str(inputs.shape))
# choose some random images to display
indices = np.arange(n_inputs)
random_indices = np.random.choice(indices, size=5)
for i, image in enumerate(digits.images[random_indices]):
plt.subplot(1, 5, i+1)
plt.axis('off')
plt.imshow(image, cmap=plt.cm.gray_r, interpolation='nearest')
plt.title("Label: %d" % digits.target[random_indices[i]])
plt.show()
from keras.utils import to_categorical
from sklearn.model_selection import train_test_split
# one-hot representation of labels
labels = to_categorical(labels)
# split into train and test data
train_size = 0.8
test_size = 1 - train_size
X_train, X_test, Y_train, Y_test = train_test_split(inputs, labels, train_size=train_size,
test_size=test_size)
import tensorflow as tf
class NeuralNetworkTensorflow:
def __init__(
self,
X_train,
Y_train,
X_test,
Y_test,
n_neurons_layer1=100,
n_neurons_layer2=50,
n_categories=2,
epochs=10,
batch_size=100,
eta=0.1,
lmbd=0.0):
# keep track of number of steps
self.global_step = tf.Variable(0, dtype=tf.int32, trainable=False, name='global_step')
self.X_train = X_train
self.Y_train = Y_train
self.X_test = X_test
self.Y_test = Y_test
self.n_inputs = X_train.shape[0]
self.n_features = X_train.shape[1]
self.n_neurons_layer1 = n_neurons_layer1
self.n_neurons_layer2 = n_neurons_layer2
self.n_categories = n_categories
self.epochs = epochs
self.batch_size = batch_size
self.iterations = self.n_inputs // self.batch_size
self.eta = eta
self.lmbd = lmbd
# build network piece by piece
# name scopes (with) are used to enforce creation of new variables
# https://www.tensorflow.org/guide/variables
self.create_placeholders()
self.create_DNN()
self.create_loss()
self.create_optimiser()
self.create_accuracy()
def create_placeholders(self):
# placeholders are fine here, but "Datasets" are the preferred method
# of streaming data into a model
with tf.name_scope('data'):
self.X = tf.placeholder(tf.float32, shape=(None, self.n_features), name='X_data')
self.Y = tf.placeholder(tf.float32, shape=(None, self.n_categories), name='Y_data')
def create_DNN(self):
with tf.name_scope('DNN'):
# the weights are stored to calculate regularization loss later
# Fully connected layer 1
self.W_fc1 = self.weight_variable([self.n_features, self.n_neurons_layer1], name='fc1', dtype=tf.float32)
b_fc1 = self.bias_variable([self.n_neurons_layer1], name='fc1', dtype=tf.float32)
a_fc1 = tf.nn.sigmoid(tf.matmul(self.X, self.W_fc1) + b_fc1)
# Fully connected layer 2
self.W_fc2 = self.weight_variable([self.n_neurons_layer1, self.n_neurons_layer2], name='fc2', dtype=tf.float32)
b_fc2 = self.bias_variable([self.n_neurons_layer2], name='fc2', dtype=tf.float32)
a_fc2 = tf.nn.sigmoid(tf.matmul(a_fc1, self.W_fc2) + b_fc2)
# Output layer
self.W_out = self.weight_variable([self.n_neurons_layer2, self.n_categories], name='out', dtype=tf.float32)
b_out = self.bias_variable([self.n_categories], name='out', dtype=tf.float32)
self.z_out = tf.matmul(a_fc2, self.W_out) + b_out
def create_loss(self):
with tf.name_scope('loss'):
softmax_loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(labels=self.Y, logits=self.z_out))
regularizer_loss_fc1 = tf.nn.l2_loss(self.W_fc1)
regularizer_loss_fc2 = tf.nn.l2_loss(self.W_fc2)
regularizer_loss_out = tf.nn.l2_loss(self.W_out)
regularizer_loss = self.lmbd*(regularizer_loss_fc1 + regularizer_loss_fc2 + regularizer_loss_out)
self.loss = softmax_loss + regularizer_loss
def create_accuracy(self):
with tf.name_scope('accuracy'):
probabilities = tf.nn.softmax(self.z_out)
predictions = tf.argmax(probabilities, axis=1)
labels = tf.argmax(self.Y, axis=1)
correct_predictions = tf.equal(predictions, labels)
correct_predictions = tf.cast(correct_predictions, tf.float32)
self.accuracy = tf.reduce_mean(correct_predictions)
def create_optimiser(self):
with tf.name_scope('optimizer'):
self.optimizer = tf.train.GradientDescentOptimizer(learning_rate=self.eta).minimize(self.loss, global_step=self.global_step)
def weight_variable(self, shape, name='', dtype=tf.float32):
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial, name=name, dtype=dtype)
def bias_variable(self, shape, name='', dtype=tf.float32):
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial, name=name, dtype=dtype)
def fit(self):
data_indices = np.arange(self.n_inputs)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for i in range(self.epochs):
for j in range(self.iterations):
chosen_datapoints = np.random.choice(data_indices, size=self.batch_size, replace=False)
batch_X, batch_Y = self.X_train[chosen_datapoints], self.Y_train[chosen_datapoints]
sess.run([DNN.loss, DNN.optimizer],
feed_dict={DNN.X: batch_X,
DNN.Y: batch_Y})
accuracy = sess.run(DNN.accuracy,
feed_dict={DNN.X: batch_X,
DNN.Y: batch_Y})
step = sess.run(DNN.global_step)
self.train_loss, self.train_accuracy = sess.run([DNN.loss, DNN.accuracy],
feed_dict={DNN.X: self.X_train,
DNN.Y: self.Y_train})
self.test_loss, self.test_accuracy = sess.run([DNN.loss, DNN.accuracy],
feed_dict={DNN.X: self.X_test,
DNN.Y: self.Y_test})
epochs = 100
batch_size = 100
n_neurons_layer1 = 100
n_neurons_layer2 = 50
n_categories = 10
eta_vals = np.logspace(-5, 1, 7)
lmbd_vals = np.logspace(-5, 1, 7)
DNN_tf = np.zeros((len(eta_vals), len(lmbd_vals)), dtype=object)
for i, eta in enumerate(eta_vals):
for j, lmbd in enumerate(lmbd_vals):
DNN = NeuralNetworkTensorflow(X_train, Y_train, X_test, Y_test,
n_neurons_layer1, n_neurons_layer2, n_categories,
epochs=epochs, batch_size=batch_size, eta=eta, lmbd=lmbd)
DNN.fit()
DNN_tf[i][j] = DNN
print("Learning rate = ", eta)
print("Lambda = ", lmbd)
print("Test accuracy: %.3f" % DNN.test_accuracy)
print()
# optional
# visual representation of grid search
# uses seaborn heatmap, could probably do this in matplotlib
import seaborn as sns
sns.set()
train_accuracy = np.zeros((len(eta_vals), len(lmbd_vals)))
test_accuracy = np.zeros((len(eta_vals), len(lmbd_vals)))
for i in range(len(eta_vals)):
for j in range(len(lmbd_vals)):
DNN = DNN_tf[i][j]
train_accuracy[i][j] = DNN.train_accuracy
test_accuracy[i][j] = DNN.test_accuracy
fig, ax = plt.subplots(figsize = (10, 10))
sns.heatmap(train_accuracy, annot=True, ax=ax, cmap="viridis")
ax.set_title("Training Accuracy")
ax.set_ylabel("$\eta$")
ax.set_xlabel("$\lambda$")
plt.show()
fig, ax = plt.subplots(figsize = (10, 10))
sns.heatmap(test_accuracy, annot=True, ax=ax, cmap="viridis")
ax.set_title("Test Accuracy")
ax.set_ylabel("$\eta$")
ax.set_xlabel("$\lambda$")
plt.show()
# optional
# we can use log files to visualize our graph in Tensorboard
writer = tf.summary.FileWriter('logs/')
writer.add_graph(tf.get_default_graph())
Keras is a high level neural network that supports Tensorflow, CTNK and Theano as backends. If you have Tensorflow installed Keras is available through the tf.keras module. If you have Anaconda installed you may run the following command
conda install keras
Alternatively, if you have Tensorflow or one of the other supported backends install you may use the pip package manager:
pip install keras
or look up the instructions here.
import tensorflow as tf
from tensorflow.keras.layers import Input
from tensorflow.keras.models import Sequential #This allows appending layers to existing models
from tensorflow.keras.layers import Dense #This allows defining the characteristics of a particular layer
from tensorflow.keras import optimizers #This allows using whichever optimiser we want (sgd,adam,RMSprop)
from tensorflow.keras import regularizers #This allows using whichever regularizer we want (l1,l2,l1_l2)
from tensorflow.keras.utils import to_categorical #This allows using categorical cross entropy as the cost function
def create_neural_network_keras(n_neurons_layer1, n_neurons_layer2, n_categories, eta, lmbd):
model = Sequential()
model.add(Dense(n_neurons_layer1, activation='sigmoid', kernel_regularizer=regularizers.l2(lmbd)))
model.add(Dense(n_neurons_layer2, activation='sigmoid', kernel_regularizer=regularizers.l2(lmbd)))
model.add(Dense(n_categories, activation='softmax'))
sgd = optimizers.SGD(lr=eta)
model.compile(loss='categorical_crossentropy', optimizer=sgd, metrics=['accuracy'])
return model
DNN_keras = np.zeros((len(eta_vals), len(lmbd_vals)), dtype=object)
for i, eta in enumerate(eta_vals):
for j, lmbd in enumerate(lmbd_vals):
DNN = create_neural_network_keras(n_neurons_layer1, n_neurons_layer2, n_categories,
eta=eta, lmbd=lmbd)
DNN.fit(X_train, Y_train, epochs=epochs, batch_size=batch_size, verbose=0)
scores = DNN.evaluate(X_test, Y_test)
DNN_keras[i][j] = DNN
print("Learning rate = ", eta)
print("Lambda = ", lmbd)
print("Test accuracy: %.3f" % scores[1])
print()
# optional
# visual representation of grid search
# uses seaborn heatmap, could probably do this in matplotlib
import seaborn as sns
sns.set()
train_accuracy = np.zeros((len(eta_vals), len(lmbd_vals)))
test_accuracy = np.zeros((len(eta_vals), len(lmbd_vals)))
for i in range(len(eta_vals)):
for j in range(len(lmbd_vals)):
DNN = DNN_keras[i][j]
train_accuracy[i][j] = DNN.evaluate(X_train, Y_train)[1]
test_accuracy[i][j] = DNN.evaluate(X_test, Y_test)[1]
fig, ax = plt.subplots(figsize = (10, 10))
sns.heatmap(train_accuracy, annot=True, ax=ax, cmap="viridis")
ax.set_title("Training Accuracy")
ax.set_ylabel("$\eta$")
ax.set_xlabel("$\lambda$")
plt.show()
fig, ax = plt.subplots(figsize = (10, 10))
sns.heatmap(test_accuracy, annot=True, ax=ax, cmap="viridis")
ax.set_title("Test Accuracy")
ax.set_ylabel("$\eta$")
ax.set_xlabel("$\lambda$")
plt.show()
import tensorflow as tf
from tensorflow.keras.layers import Input
from tensorflow.keras.models import Sequential #This allows appending layers to existing models
from tensorflow.keras.layers import Dense #This allows defining the characteristics of a particular layer
from tensorflow.keras import optimizers #This allows using whichever optimiser we want (sgd,adam,RMSprop)
from tensorflow.keras import regularizers #This allows using whichever regularizer we want (l1,l2,l1_l2)
from tensorflow.keras.utils import to_categorical #This allows using categorical cross entropy as the cost function
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split as splitter
from sklearn.datasets import load_breast_cancer
import pickle
import os
"""Load breast cancer dataset"""
np.random.seed(0) #create same seed for random number every time
cancer=load_breast_cancer() #Download breast cancer dataset
inputs=cancer.data #Feature matrix of 569 rows (samples) and 30 columns (parameters)
outputs=cancer.target #Label array of 569 rows (0 for benign and 1 for malignant)
labels=cancer.feature_names[0:30]
print('The content of the breast cancer dataset is:') #Print information about the datasets
print(labels)
print('-------------------------')
print("inputs = " + str(inputs.shape))
print("outputs = " + str(outputs.shape))
print("labels = "+ str(labels.shape))
x=inputs #Reassign the Feature and Label matrices to other variables
y=outputs
#%%
# Visualisation of dataset (for correlation analysis)
plt.figure()
plt.scatter(x[:,0],x[:,2],s=40,c=y,cmap=plt.cm.Spectral)
plt.xlabel('Mean radius',fontweight='bold')
plt.ylabel('Mean perimeter',fontweight='bold')
plt.show()
plt.figure()
plt.scatter(x[:,5],x[:,6],s=40,c=y, cmap=plt.cm.Spectral)
plt.xlabel('Mean compactness',fontweight='bold')
plt.ylabel('Mean concavity',fontweight='bold')
plt.show()
plt.figure()
plt.scatter(x[:,0],x[:,1],s=40,c=y,cmap=plt.cm.Spectral)
plt.xlabel('Mean radius',fontweight='bold')
plt.ylabel('Mean texture',fontweight='bold')
plt.show()
plt.figure()
plt.scatter(x[:,2],x[:,1],s=40,c=y,cmap=plt.cm.Spectral)
plt.xlabel('Mean perimeter',fontweight='bold')
plt.ylabel('Mean compactness',fontweight='bold')
plt.show()
# Generate training and testing datasets
#Select features relevant to classification (texture,perimeter,compactness and symmetery)
#and add to input matrix
temp1=np.reshape(x[:,1],(len(x[:,1]),1))
temp2=np.reshape(x[:,2],(len(x[:,2]),1))
X=np.hstack((temp1,temp2))
temp=np.reshape(x[:,5],(len(x[:,5]),1))
X=np.hstack((X,temp))
temp=np.reshape(x[:,8],(len(x[:,8]),1))
X=np.hstack((X,temp))
X_train,X_test,y_train,y_test=splitter(X,y,test_size=0.1) #Split datasets into training and testing
y_train=to_categorical(y_train) #Convert labels to categorical when using categorical cross entropy
y_test=to_categorical(y_test)
del temp1,temp2,temp
# %%
# Define tunable parameters"
eta=np.logspace(-3,-1,3) #Define vector of learning rates (parameter to SGD optimiser)
lamda=0.01 #Define hyperparameter
n_layers=2 #Define number of hidden layers in the model
n_neuron=np.logspace(0,3,4,dtype=int) #Define number of neurons per layer
epochs=100 #Number of reiterations over the input data
batch_size=100 #Number of samples per gradient update
# %%
"""Define function to return Deep Neural Network model"""
def NN_model(inputsize,n_layers,n_neuron,eta,lamda):
model=Sequential()
for i in range(n_layers): #Run loop to add hidden layers to the model
if (i==0): #First layer requires input dimensions
model.add(Dense(n_neuron,activation='relu',kernel_regularizer=regularizers.l2(lamda),input_dim=inputsize))
else: #Subsequent layers are capable of automatic shape inferencing
model.add(Dense(n_neuron,activation='relu',kernel_regularizer=regularizers.l2(lamda)))
model.add(Dense(2,activation='softmax')) #2 outputs - ordered and disordered (softmax for prob)
sgd=optimizers.SGD(lr=eta)
model.compile(loss='categorical_crossentropy',optimizer=sgd,metrics=['accuracy'])
return model
Train_accuracy=np.zeros((len(n_neuron),len(eta))) #Define matrices to store accuracy scores as a function
Test_accuracy=np.zeros((len(n_neuron),len(eta))) #of learning rate and number of hidden neurons for
for i in range(len(n_neuron)): #run loops over hidden neurons and learning rates to calculate
for j in range(len(eta)): #accuracy scores
DNN_model=NN_model(X_train.shape[1],n_layers,n_neuron[i],eta[j],lamda)
DNN_model.fit(X_train,y_train,epochs=epochs,batch_size=batch_size,verbose=1)
Train_accuracy[i,j]=DNN_model.evaluate(X_train,y_train)[1]
Test_accuracy[i,j]=DNN_model.evaluate(X_test,y_test)[1]
def plot_data(x,y,data,title=None):
# plot results
fontsize=16
fig = plt.figure()
ax = fig.add_subplot(111)
cax = ax.matshow(data, interpolation='nearest', vmin=0, vmax=1)
cbar=fig.colorbar(cax)
cbar.ax.set_ylabel('accuracy (%)',rotation=90,fontsize=fontsize)
cbar.set_ticks([0,.2,.4,0.6,0.8,1.0])
cbar.set_ticklabels(['0%','20%','40%','60%','80%','100%'])
# put text on matrix elements
for i, x_val in enumerate(np.arange(len(x))):
for j, y_val in enumerate(np.arange(len(y))):
c = "${0:.1f}\\%$".format( 100*data[j,i])
ax.text(x_val, y_val, c, va='center', ha='center')
# convert axis vaues to to string labels
x=[str(i) for i in x]
y=[str(i) for i in y]
ax.set_xticklabels(['']+x)
ax.set_yticklabels(['']+y)
ax.set_xlabel('$\\mathrm{learning\\ rate}$',fontsize=fontsize)
ax.set_ylabel('$\\mathrm{hidden\\ neurons}$',fontsize=fontsize)
if title is not None:
ax.set_title(title)
plt.tight_layout()
plt.show()
plot_data(eta,n_neuron,Train_accuracy, 'training')
plot_data(eta,n_neuron,Test_accuracy, 'testing')
The Back propagation algorithm we derived above works by going from the output layer to the input layer, propagating the error gradient on the way. Once the algorithm has computed the gradient of the cost function with regards to each parameter in the network, it uses these gradients to update each parameter with a Gradient Descent (GD) step.
Unfortunately for us, the gradients often get smaller and smaller as the algorithm progresses down to the first hidden layers. As a result, the GD update leaves the lower layer connection weights virtually unchanged, and training never converges to a good solution. This is known in the literature as the vanishing gradients problem.
In other cases, the opposite can happen, namely the the gradients can grow bigger and bigger. The result is that many of the layers get large updates of the weights the algorithm diverges. This is the exploding gradients problem, which is mostly encountered in recurrent neural networks. More generally, deep neural networks suffer from unstable gradients, different layers may learn at widely different speeds
Although this unfortunate behavior has been empirically observed for quite a while (it was one of the reasons why deep neural networks were mostly abandoned for a long time), it is only around 2010 that significant progress was made in understanding it.
A paper titled Understanding the Difficulty of Training Deep Feedforward Neural Networks by Xavier Glorot and Yoshua Bengio found that the problems with the popular logistic sigmoid activation function and the weight initialization technique that was most popular at the time, namely random initialization using a normal distribution with a mean of 0 and a standard deviation of 1.
They showed that with this activation function and this initialization scheme, the variance of the outputs of each layer is much greater than the variance of its inputs. Going forward in the network, the variance keeps increasing after each layer until the activation function saturates at the top layers. This is actually made worse by the fact that the logistic function has a mean of 0.5, not 0 (the hyperbolic tangent function has a mean of 0 and behaves slightly better than the logistic function in deep networks).
Looking at the logistic activation function, when inputs become large (negative or positive), the function saturates at 0 or 1, with a derivative extremely close to 0. Thus when backpropagation kicks in, it has virtually no gradient to propagate back through the network, and what little gradient exists keeps getting diluted as backpropagation progresses down through the top layers, so there is really nothing left for the lower layers.
In their paper, Glorot and Bengio propose a way to significantly alleviate this problem. We need the signal to flow properly in both directions: in the forward direction when making predictions, and in the reverse direction when backpropagating gradients. We don’t want the signal to die out, nor do we want it to explode and saturate. For the signal to flow properly, the authors argue that we need the variance of the outputs of each layer to be equal to the variance of its inputs, and we also need the gradients to have equal variance before and after flowing through a layer in the reverse direction.
One of the insights in the 2010 paper by Glorot and Bengio was that the vanishing/exploding gradients problems were in part due to a poor choice of activation function. Until then most people had assumed that if Nature had chosen to use roughly sigmoid activation functions in biological neurons, they must be an excellent choice. But it turns out that other activation functions behave much better in deep neural networks, in particular the ReLU activation function, mostly because it does not saturate for positive values (and also because it is quite fast to compute).
The ReLU activation function suffers from a problem known as the dying ReLUs: during training, some neurons effectively die, meaning they stop outputting anything other than 0.
In some cases, you may find that half of your network’s neurons are dead, especially if you used a large learning rate. During training, if a neuron’s weights get updated such that the weighted sum of the neuron’s inputs is negative, it will start outputting 0. When this happen, the neuron is unlikely to come back to life since the gradient of the ReLU function is 0 when its input is negative.
To solve this problem, nowadays practitioners use a variant of the ReLU function, such as the leaky ReLU discussed above or the so-called exponential linear unit (ELU) function $$ ELU(z) = \left\{\begin{array}{cc} \alpha\left( \exp{(z)}-1\right) & z < 0,\\ z & z \ge 0.\end{array}\right. $$
In general it seems that the ELU activation function is better than the leaky ReLU function (and its variants), which is better than ReLU. ReLU performs better than \( \tanh \) which in turn performs better than the logistic function.
If runtime performance is an issue, then you may opt for the leaky ReLU function over the ELU function If you don’t want to tweak yet another hyperparameter, you may just use the default \( \alpha \) of \( 0.01 \) for the leaky ReLU, and \( 1 \) for ELU. If you have spare time and computing power, you can use cross-validation or bootstrap to evaluate other activation functions.
The first thing we would like to do is divide the data into two or three parts. A training set, a validation or dev (development) set, and a test set. The test set is the data on which we want to make predictions. The dev set is a subset of the training data we use to check how well we are doing out-of-sample, after training the model on the training dataset. We use the validation error as a proxy for the test error in order to make tweaks to our model. It is crucial that we do not use any of the test data to train the algorithm. This is a cardinal sin in ML. Then:
However, sometimes the training data and test data differ in subtle ways because, for example, they are collected using slightly different methods, or because it is cheaper to collect data in one way versus another. In this case, there can be a mismatch between the training and test data. This can lead to the neural network overfitting these small differences between the test and training sets, and a poor performance on the test set despite having a good performance on the validation set. To rectify this, Andrew Ng suggests making two validation or dev sets, one constructed from the training data and one constructed from the test data. The difference between the performance of the algorithm on these two validation sets quantifies the train-test mismatch. This can serve as another important diagnostic when using DNNs for supervised learning.
Like all statistical methods, supervised learning using neural networks has important limitations. This is especially important when one seeks to apply these methods, especially to physics problems. Like all tools, DNNs are not a universal solution. Often, the same or better performance on a task can be achieved by using a few hand-engineered features (or even a collection of random features).
Here we list some of the important limitations of supervised neural network based models.
Pulsar classification can be one of the best training grounds for performing machine learning in astrophysics. These pulsars are said to be pulsating radio sources, which have now been identified to be caused by rapidly rotating highly magnetized neutron stars and are detectable here on Earth . One of the characteristic properties of these pulsars is that they exhibit periodic bursts of emission produced by their radio emitting jets. The direction of their emission also rotates with them and sweep the sky like a lighthouse. This gives astronomers information about the phenomenon as they observe a pulse of radio emission each time one of the jets points towards the Earth.
The study and detection of pulsars provide a wealth of information about the physics of neutron stars. They are also used as probes of stellar evolution. In addition, they are being used to test or verify some concepts in general relativity due to their extremely high densities. These allowed them to be good observables in detecting and mapping gravitational wave signatures. One problem, however, is that they are very difficult to identify in the large stream of data from radio telescopes. Moreover, a lot of man-made sources of radio frequency interference are also present, which can produce the same signals as pulsars. Hence, the classification of pulsars from possible candidate data is of great importance.
In reality, pulsars are very weak radio sources. They are classified from a given data sample by first extracting information from the pool of data and then identifying which features or characteristics are relevant. Since the individual pulses are very much different, astronomers particularly stack them up and generate an integrated pulse profile for pulsar classification. This profile is the coherent addition of thousands of pulses together in a process known as folding. Moreover, pulses will arrive at various times across different radio frequencies. The delay of these pulses from frequency to frequency is called dispersion and is said to be caused by the ionized inter-stellar medium. The method usually employed by astronomers is that they fit for the shape of the delay as to reduce its negative effect. However, as with all kinds of fitting procedures, there would always be an uncertainty associated with it. This is expressed in the so-called DM-SNR (dispersion-measure-signal-to-noise-ratio) curve. Both the integrated profile curve and DM-SNR curve are used in identifying possible pulsar candidates. These curves provide eight numerical characteristic features as depicted and listed below.
For this dataset, there is already an initial classification of the potential pulsar candidates as pulsars and non-pulsars by the astronomy community. We aim here to perform machine learning and try to build a model that can detect patterns within the data. This will eventually lead to the correct classification of new potential pulsars that will soon be observed.
# reading and handling the data
import pandas as pd
import warnings
warnings.filterwarnings("ignore")
data = pd.read_csv("pulsar_stars.csv")
# print a part of the dataset
data.head()
print ("Number of rows :",data.shape[0])
print ("Number of columns :",data.shape[1])
print ("data info :",data.info())
print (data.isnull().sum())
# import packages for plotting
import matplotlib.pyplot as plt
import seaborn as sns
plt.figure(figsize=(12,6))
plt.subplot(121)
ax = sns.countplot(y = data["target_class"],
palette=["r","g"],
linewidth=1,
edgecolor="k"*2)
for i,j in enumerate(data["target_class"].value_counts().values):
ax.text(.7,i,j,weight = "bold",fontsize = 27)
plt.title("Count for target variable in dataset")
plt.subplot(122)
plt.pie(data["target_class"].value_counts().values,
labels=["not pulsar stars","pulsar stars"],
autopct="%1.0f%%",wedgeprops={"linewidth":2,"edgecolor":"white"})
my_circ = plt.Circle((0,0),.7,color = "white")
plt.gca().add_artist(my_circ)
plt.subplots_adjust(wspace = .2)
plt.title("Proportion of target variable in dataset")
plt.show()
The dataset contains 17898 candidates for which only 1639 (\( \approx 9\% \)) are classified as real pulsars. In addition, the dataset consists of features rather than raw data from observations. The eight features considered in the study are given above as column headers. The first four are the usual statistics obtained from the integrated pulse profile. A class label (targetclass) is also included which determines if the candidate is considered to be a pulsar (1) or not (0). This serves as our target column for the analysis.
When dealing with all sorts of data, an important first step is to often get a sense on how the variables are distributed. As seen above, the dataset can be considered clean and complete as there are no missing data and the number of features is relatively small. This reduces extra steps towards feature engineering as there is not much to do for artificial design features. Thus, we can see readily that the preprocessing stage only involves two main issues. First is the possible problem of overfitting since the difference between the numbers of candidates identified as pulsars and non-pulsars is large, with a ratio of about 1:10. The other issue is the huge distribution for the range differences of the eight features. This is evident in the figures here. The plots were done using the distplot() function in the package seaborn. This draws a histogram and fit a kernel density estimate (KDE).
# import package
import itertools
# rename column headers for convenience
data = data.rename(columns={" Mean of the integrated profile": "Mean profile", " Standard deviation of the integrated profile": "StD profile",
" Excess kurtosis of the integrated profile": "Kurtosis profile", " Skewness of the integrated profile": "Skewness profile",
" Mean of the DM-SNR curve": "Mean DM-SNR", " Standard deviation of the DM-SNR curve": "StD DM-SNR",
" Excess kurtosis of the DM-SNR curve": "Kurtosis DM-SNR", " Skewness of the DM-SNR curve": "Skewness DM-SNR",
"target_class": "Target class"})
# distribution of variable in the dataset
columns = ['Mean profile', 'StD profile', 'Kurtosis profile', 'Skewness profile',
'Mean DM-SNR', 'StD DM-SNR', 'Kurtosis DM-SNR',
'Skewness DM-SNR']
length = len(columns)
colors = ["r","g","b","m","y","c","k","orange"]
plt.figure(figsize=(13,20))
for i,j,k in itertools.zip_longest(columns,range(length),colors):
plt.subplot(length/2,length/4,j+1)
sns.distplot(data[i],color=k)
plt.title(i)
plt.subplots_adjust(hspace = .3)
plt.axvline(data[i].mean(),color = "k",linestyle="dashed",label="MEAN")
plt.axvline(data[i].std(),color = "b",linestyle="dotted",label="STANDARD DEVIATION")
plt.legend(loc="upper right")
Before delving into any analysis, we would like to decrease the amount of data to look at. This can be achieved by performing a correlation plot. As seen in Figure 5, the features that correlate the most with the class (pulsar or non-pulsar) are the mean, the excess kurtosis, and the skewness of the integrated profile. We could choose to only analyze these, but this would mean that pulsars can be identified with only one of the two plots that astrophysicists use to classify the data. In this case, colinearity may become a problem since these features are strongly correlated with each other.
# correlation matrix
corr_matrix = data.corr()
# Pair plots
sns.pairplot(data,hue = "Target class")
plt.title("Pair plot for variables")
# plt.savefig('pairplot.png',bbox_inches='tight')
plt.show()
# Violin Plot
columns = [x for x in data.columns if x not in ["Target class"]]
length = len(columns)
plt.figure(figsize=(13,25))
for i,j in itertools.zip_longest(columns,range(length)):
plt.subplot(length/2,length/4,j+1)
sns.violinplot(x=data["Target class"],y=data[i],
palette=["Orangered","lime"],alpha=.5)
plt.title(i)
#plt.savefig('violinplot.png',bbox_inches='tight')
plt.show()
# Logistc regression
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.model_selection import KFold
from sklearn.metrics import confusion_matrix
# We define the hyperparameters to be used
nlambdas = 500 # why not? the code runs relatively fast
lmbdas = np.logspace(-5, 5, nlambdas)
kfold = KFold(n_splits = 5) #cross validation spliting
# We preallocate data
# true values that will be found later
train_accuracy=np.zeros(lmbdas.shape,np.float64)
test_accuracy=np.zeros(lmbdas.shape,np.float64)
train_red_accuracy=np.zeros(lmbdas.shape,np.float64)
test_red_accuracy=np.zeros(lmbdas.shape,np.float64)
# dummy arrays to be averaged later on
train_accuracy_d=np.zeros(5,np.float64)
test_accuracy_d=np.zeros(5,np.float64)
train_red_accuracy_d=np.zeros(5,np.float64)
test_red_accuracy_d=np.zeros(5,np.float64)
# We create the design matrix X and separate the labels into Y
x_fea = [x for x in data.columns if x not in ['Target class']]
#print(x_fea)
X = np.zeros((data.shape[0],data.shape[1]-1))
X_red = np.zeros((data.shape[0],3))
Y = np.zeros(data.shape[0])
for i,feature in enumerate(x_fea): # Here we just take the variables of interest
X[:,i] = data[feature]
if 'Mean profile' == feature:
X_red[:,0]
if 'Kurtosis profile' == feature:
X_red[:,1]
if 'Skewness profile'== feature:
X_red[:,2]
Y[:] = data['Target class']
# We perform a logistic regression for each value of lambda
for i,lmbda in enumerate(lmbdas):
#define model
logreg = LogisticRegression(C=1.0/lmbda,solver='liblinear')
# Perform the cross-validation
j = 0
for train_inds, test_inds in kfold.split(X):
# Do the split
X_train = X[train_inds]
X_red_train = X_red[train_inds]
Y_train = Y[train_inds]
X_test = X[test_inds]
X_red_test = X_red[test_inds]
Y_test = Y[test_inds]
# We will scale the data
scaler = StandardScaler()
scaler.fit(X_train)
# first on full data
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
# then rescale and do on reduced data
scaler.fit(X_red_train)
X_red_train = scaler.transform(X_red_train)
X_red_test = scaler.transform(X_red_test)
del scaler
# calculate accuracies for the k fold
logreg.fit(X_train, Y_train)
train_accuracy_d[j]=logreg.score(X_train,Y_train)
test_accuracy_d[j]=logreg.score(X_test,Y_test)
logreg.fit(X_red_train, Y_train)
train_red_accuracy_d[j]=logreg.score(X_red_train,Y_train)
test_red_accuracy_d[j]=logreg.score(X_red_test,Y_test)
j += 1
del X_red_train,X_red_test,X_train,Y_train,X_test,Y_test # delete useless data
#Average to get accuracy values
train_accuracy[i]=np.mean(train_accuracy_d)
test_accuracy[i]=np.mean(test_accuracy_d)
train_red_accuracy[i]=np.mean(train_red_accuracy_d)
test_red_accuracy[i]=np.mean(test_red_accuracy_d)
plt.figure(figsize=(15,7))
plt.semilogx(lmbdas,train_accuracy,label='train')
plt.semilogx(lmbdas,test_accuracy,label='test')
plt.semilogx(lmbdas,train_red_accuracy,label='train reduced')
plt.semilogx(lmbdas,test_red_accuracy,'--',label='test reduced')
plt.xlabel('$\\lambda$')
plt.ylabel('$\\mathrm{accuracy}$')
plt.grid()
plt.legend()
plt.show()
# Neural Network
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
import itertools
from PIL import Image
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix,accuracy_score
from sklearn.neural_network import MLPClassifier
warnings.filterwarnings("ignore")
#Split data with 20% of test data:
np.random.seed(2018)
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size = 0.2, random_state = 66)
# Define the learning rate, hyperparameter using NUMPY
eta_vals = np.logspace(-5, 1, 7)
lmbd_vals = np.logspace(-5, 1, 7)
n_hidden_neurons = 50
epochs = 100
# Use scikit learn for neural network
DNN_scikit = np.zeros((len(eta_vals), len(lmbd_vals)), dtype=object)
for i, eta in enumerate(eta_vals):
for j, lmbd in enumerate(lmbd_vals):
dnn = MLPClassifier(hidden_layer_sizes=(n_hidden_neurons), activation='logistic',
alpha=lmbd, learning_rate_init=eta, max_iter=epochs, solver='adam')
dnn.fit(X_train, y_train)
DNN_scikit[i][j] = dnn
# just uncomment below to print the accuracy scores
#print("Learning rate = ", eta)
#print("Lambda = ", lmbd)
#print("Accuracy score on test set: ", dnn.score(X_test, y_test))
#print()
#Plot the accuracy as function of learning rate and hyperparameter
# just uncomment the lines below to generate the plots (ctrl + /)
sns.set()
train_accuracy = np.zeros((len(eta_vals), len(lmbd_vals)))
test_accuracy = np.zeros((len(eta_vals), len(lmbd_vals)))
for i in range(len(eta_vals)):
for j in range(len(lmbd_vals)):
dnn = DNN_scikit[i][j]
train_pred = dnn.predict(X_train)
test_pred = dnn.predict(X_test)
train_accuracy[i][j] = accuracy_score(y_train, train_pred)
test_accuracy[i][j] = accuracy_score(y_test, test_pred)
fig, ax = plt.subplots(figsize = (10, 10))
sns.heatmap(train_accuracy, annot=True,annot_kws={"size": 18}, ax=ax, cmap="viridis")
ax.set_title("Training Accuracy",fontsize=18)
ax.set_ylabel("$\eta$",fontsize=18)
ax.set_yticklabels(eta_vals)
ax.set_xlabel("$\lambda$",fontsize=18)
ax.set_xticklabels(lmbd_vals)
plt.tick_params(labelsize=18)
fig, ax = plt.subplots(figsize = (10, 10))
sns.heatmap(test_accuracy, annot=True,annot_kws={"size": 18}, ax=ax, cmap="viridis")
ax.set_title("Test Accuracy",fontsize=18)
ax.set_ylabel("$\eta$",fontsize=18)
ax.set_yticklabels(eta_vals)
ax.set_xlabel("$\lambda$",fontsize=18)
ax.set_xticklabels(lmbd_vals)
plt.tick_params(labelsize=18)
plt.show()
#Plot confusion matrix at optimal values of learning rate and hyperameter
# just uncomment the lines below to generate the plots (ctrl + /)
dnn = MLPClassifier(hidden_layer_sizes=(n_hidden_neurons), activation='logistic',alpha=0.001, learning_rate_init=0.001, max_iter=epochs, solver='adam')
dnn.fit(X_train,y_train)
y_pred=dnn.predict(X_test)
fig1, ax = plt.subplots(figsize = (13,10))
sns.heatmap(confusion_matrix(y_test,y_pred),annot=True,fmt = "d",linecolor="k",linewidths=3)
ax.set_xlabel('True label',fontsize=18)
ax.set_ylabel('Predicted label',fontsize=18)
ax.set_title("CONFUSION MATRIX",fontsize=20)
plt.tick_params(labelsize=18)
plt.show()
# Feature importance -->weights
coef=dnn.coefs_[0]
print (coef)
Convolutional neural networks (CNNs) were developed during the last decade of the previous century, with a focus on character recognition tasks. Nowadays, CNNs are a central element in the spectacular success of dee learning methods. The success in for example image classifications have made them a central tool for most machine learning practitioners.
CNNs are very similar to ordinary Neural Networks. They are made up of neurons that have learnable weights and biases. Each neuron receives some inputs, performs a dot product and optionally follows it with a non-linearity. The whole network still expresses a single differentiable score function: from the raw image pixels on one end to class scores at the other. And they still have a loss function (for example Softmax) on the last (fully-connected) layer and all the tips/tricks we developed for learning regular Neural Networks still apply (back propagation, gradient descent etc etc).
What is the difference? CNN architectures make the explicit assumption that the inputs are images, which allows us to encode certain properties into the architecture. These then make the forward function more efficient to implement and vastly reduce the amount of parameters in the network.
Here we provide only a superficial overview, for the more interested, we recommend highly the course IN5400 – Machine Learning for Image Analysis and the slides of CS231.
Another good read is the article here https://arxiv.org/pdf/1603.07285.pdf.
As an example, consider an image of size \( 32\times 32\times 3 \) (32 wide, 32 high, 3 color channels), so a single fully-connected neuron in a first hidden layer of a regular Neural Network would have \( 32\times 32\times 3 = 3072 \) weights. This amount still seems manageable, but clearly this fully-connected structure does not scale to larger images. For example, an image of more respectable size, say \( 200\times 200\times 3 \), would lead to neurons that have \( 200\times 200\times 3 = 120,000 \) weights.
We could have several such neurons, and the parameters would add up quickly! Clearly, this full connectivity is wasteful and the huge number of parameters would quickly lead to possible overfitting.
Figure 1: A regular 3-layer Neural Network.

Convolutional Neural Networks take advantage of the fact that the input consists of images and they constrain the architecture in a more sensible way.
In particular, unlike a regular Neural Network, the layers of a CNN have neurons arranged in 3 dimensions: width, height, depth. (Note that the word depth here refers to the third dimension of an activation volume, not to the depth of a full Neural Network, which can refer to the total number of layers in a network.)
To understand it better, the above example of an image with an input volume of activations has dimensions \( 32\times 32\times 3 \) (width, height, depth respectively).
The neurons in a layer will only be connected to a small region of the layer before it, instead of all of the neurons in a fully-connected manner. Moreover, the final output layer could for this specific image have dimensions \( 1\times 1 \times 10 \), because by the end of the CNN architecture we will reduce the full image into a single vector of class scores, arranged along the depth dimension.
Figure 2: A CNN arranges its neurons in three dimensions (width, height, depth), as visualized in one of the layers. Every layer of a CNN transforms the 3D input volume to a 3D output volume of neuron activations. In this example, the red input layer holds the image, so its width and height would be the dimensions of the image, and the depth would be 3 (Red, Green, Blue channels).
A simple CNN is a sequence of layers, and every layer of a CNN transforms one volume of activations to another through a differentiable function. We use three main types of layers to build CNN architectures: Convolutional Layer, Pooling Layer, and Fully-Connected Layer (exactly as seen in regular Neural Networks). We will stack these layers to form a full CNN architecture.
A simple CNN for image classification could have the architecture:
CNNs transform the original image layer by layer from the original pixel values to the final class scores.
Observe that some layers contain parameters and other don’t. In particular, the CNN layers perform transformations that are a function of not only the activations in the input volume, but also of the parameters (the weights and biases of the neurons). On the other hand, the RELU/POOL layers will implement a fixed function. The parameters in the CONV/FC layers will be trained with gradient descent so that the class scores that the CNN computes are consistent with the labels in the training set for each image.
In summary:
As discussed above, CNNs are neural networks built from the assumption that the inputs to the network are 2D images. This is important because the number of features or pixels in images grows very fast with the image size, and an enormous number of weights and biases are needed in order to build an accurate network.
As before, we still have our input, a hidden layer and an output. What's novel about convolutional networks are the convolutional and pooling layers stacked in pairs between the input and the hidden layer. In addition, the data is no longer represented as a 2D feature matrix, instead each input is a number of 2D matrices, typically 1 for each color dimension (Red, Green, Blue).
It means that to represent the entire dataset of images, we require a 4D matrix or tensor. This tensor has the dimensions: $$ (n_{inputs},\, n_{pixels, width},\, n_{pixels, height},\, depth) . $$
The MNIST dataset consists of grayscale images with a pixel size of \( 28\times 28 \), meaning we require \( 28 \times 28 = 724 \) weights to each neuron in the first hidden layer.
If we were to analyze images of size \( 128\times 128 \) we would require \( 128 \times 128 = 16384 \) weights to each neuron. Even worse if we were dealing with color images, as most images are, we have an image matrix of size \( 128\times 128 \) for each color dimension (Red, Green, Blue), meaning 3 times the number of weights \( = 49152 \) are required for every single neuron in the first hidden layer.
Therefore, instead of connecting every single pixel to a neuron in the first hidden layer, as we have previously done with deep neural networks, we can instead connect each neuron to a small part of the image (in all 3 RGB depth dimensions). The size of each small area is fixed, and known as a receptive.
A convolution is performed on the image which outputs a 3D volume of neurons. The weights to the input are arranged in a number of 2D matrices, known as filters.
Each filter slides along the input image, taking the dot product between each small part of the image and the filter, in all depth dimensions. This is then passed through a non-linear function, typically the Rectified Linear (ReLu) function, which serves as the activation of the neurons in the first convolutional layer. This is further passed through a pooling layer, which reduces the size of the convolutional layer, e.g. by taking the maximum or average across some small regions, and this serves as input to the next convolutional layer.
By systematically reducing the size of the input volume, through convolution and pooling, the network should create representations of small parts of the input, and then from them assemble representations of larger areas. The final pooling layer is flattened to serve as input to a hidden layer, such that each neuron in the final pooling layer is connected to every single neuron in the hidden layer. This then serves as input to the output layer, e.g. a softmax output for classification.
# import necessary packages
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
# ensure the same random numbers appear every time
np.random.seed(0)
# display images in notebook
%matplotlib inline
plt.rcParams['figure.figsize'] = (12,12)
# download MNIST dataset
digits = datasets.load_digits()
# define inputs and labels
inputs = digits.images
labels = digits.target
# RGB images have a depth of 3
# our images are grayscale so they should have a depth of 1
inputs = inputs[:,:,:,np.newaxis]
print("inputs = (n_inputs, pixel_width, pixel_height, depth) = " + str(inputs.shape))
print("labels = (n_inputs) = " + str(labels.shape))
# choose some random images to display
n_inputs = len(inputs)
indices = np.arange(n_inputs)
random_indices = np.random.choice(indices, size=5)
for i, image in enumerate(digits.images[random_indices]):
plt.subplot(1, 5, i+1)
plt.axis('off')
plt.imshow(image, cmap=plt.cm.gray_r, interpolation='nearest')
plt.title("Label: %d" % digits.target[random_indices[i]])
plt.show()
import tensorflow as tf
from tensorflow.keras.layers import Input
from tensorflow.keras.models import Sequential #This allows appending layers to existing models
from tensorflow.keras.layers import Dense #This allows defining the characteristics of a particular layer
from tensorflow.keras import optimizers #This allows using whichever optimiser we want (sgd,adam,RMSprop)
from tensorflow.keras import regularizers #This allows using whichever regularizer we want (l1,l2,l1_l2)
from tensorflow.keras.utils import to_categorical #This allows using categorical cross entropy as the cost function
from sklearn.model_selection import train_test_split
# representation of labels
labels = to_categorical(labels)
# split into train and test data
# one-liner from scikit-learn library
train_size = 0.8
test_size = 1 - train_size
X_train, X_test, Y_train, Y_test = train_test_split(inputs, labels, train_size=train_size,
test_size=test_size)
We need to define model and architecture and choose cost function and optmizer.
import tensorflow as tf
class ConvolutionalNeuralNetworkTensorflow:
def __init__(
self,
X_train,
Y_train,
X_test,
Y_test,
n_filters=10,
n_neurons_connected=50,
n_categories=10,
receptive_field=3,
stride=1,
padding=1,
epochs=10,
batch_size=100,
eta=0.1,
lmbd=0.0):
self.global_step = tf.Variable(0, dtype=tf.int32, trainable=False, name='global_step')
self.X_train = X_train
self.Y_train = Y_train
self.X_test = X_test
self.Y_test = Y_test
self.n_inputs, self.input_width, self.input_height, self.depth = X_train.shape
self.n_filters = n_filters
self.n_downsampled = int(self.input_width*self.input_height*n_filters / 4)
self.n_neurons_connected = n_neurons_connected
self.n_categories = n_categories
self.receptive_field = receptive_field
self.stride = stride
self.strides = [stride, stride, stride, stride]
self.padding = padding
self.epochs = epochs
self.batch_size = batch_size
self.iterations = self.n_inputs // self.batch_size
self.eta = eta
self.lmbd = lmbd
self.create_placeholders()
self.create_CNN()
self.create_loss()
self.create_optimiser()
self.create_accuracy()
def create_placeholders(self):
with tf.name_scope('data'):
self.X = tf.placeholder(tf.float32, shape=(None, self.input_width, self.input_height, self.depth), name='X_data')
self.Y = tf.placeholder(tf.float32, shape=(None, self.n_categories), name='Y_data')
def create_CNN(self):
with tf.name_scope('CNN'):
# Convolutional layer
self.W_conv = self.weight_variable([self.receptive_field, self.receptive_field, self.depth, self.n_filters], name='conv', dtype=tf.float32)
b_conv = self.weight_variable([self.n_filters], name='conv', dtype=tf.float32)
z_conv = tf.nn.conv2d(self.X, self.W_conv, self.strides, padding='SAME', name='conv') + b_conv
a_conv = tf.nn.relu(z_conv)
# 2x2 max pooling
a_pool = tf.nn.max_pool(a_conv, [1, 2, 2, 1], [1, 2, 2, 1], padding='SAME', name='pool')
# Fully connected layer
a_pool_flat = tf.reshape(a_pool, [-1, self.n_downsampled])
self.W_fc = self.weight_variable([self.n_downsampled, self.n_neurons_connected], name='fc', dtype=tf.float32)
b_fc = self.bias_variable([self.n_neurons_connected], name='fc', dtype=tf.float32)
a_fc = tf.nn.relu(tf.matmul(a_pool_flat, self.W_fc) + b_fc)
# Output layer
self.W_out = self.weight_variable([self.n_neurons_connected, self.n_categories], name='out', dtype=tf.float32)
b_out = self.bias_variable([self.n_categories], name='out', dtype=tf.float32)
self.z_out = tf.matmul(a_fc, self.W_out) + b_out
def create_loss(self):
with tf.name_scope('loss'):
softmax_loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(labels=self.Y, logits=self.z_out))
regularizer_loss_conv = tf.nn.l2_loss(self.W_conv)
regularizer_loss_fc = tf.nn.l2_loss(self.W_fc)
regularizer_loss_out = tf.nn.l2_loss(self.W_out)
regularizer_loss = self.lmbd*(regularizer_loss_conv + regularizer_loss_fc + regularizer_loss_out)
self.loss = softmax_loss + regularizer_loss
def create_accuracy(self):
with tf.name_scope('accuracy'):
probabilities = tf.nn.softmax(self.z_out)
predictions = tf.argmax(probabilities, 1)
labels = tf.argmax(self.Y, 1)
correct_predictions = tf.equal(predictions, labels)
correct_predictions = tf.cast(correct_predictions, tf.float32)
self.accuracy = tf.reduce_mean(correct_predictions)
def create_optimiser(self):
with tf.name_scope('optimizer'):
self.optimizer = tf.train.GradientDescentOptimizer(learning_rate=self.eta).minimize(self.loss, global_step=self.global_step)
def weight_variable(self, shape, name='', dtype=tf.float32):
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial, name=name, dtype=dtype)
def bias_variable(self, shape, name='', dtype=tf.float32):
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial, name=name, dtype=dtype)
def fit(self):
data_indices = np.arange(self.n_inputs)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for i in range(self.epochs):
for j in range(self.iterations):
chosen_datapoints = np.random.choice(data_indices, size=self.batch_size, replace=False)
batch_X, batch_Y = self.X_train[chosen_datapoints], self.Y_train[chosen_datapoints]
sess.run([CNN.loss, CNN.optimizer],
feed_dict={CNN.X: batch_X,
CNN.Y: batch_Y})
accuracy = sess.run(CNN.accuracy,
feed_dict={CNN.X: batch_X,
CNN.Y: batch_Y})
step = sess.run(CNN.global_step)
self.train_loss, self.train_accuracy = sess.run([CNN.loss, CNN.accuracy],
feed_dict={CNN.X: self.X_train,
CNN.Y: self.Y_train})
self.test_loss, self.test_accuracy = sess.run([CNN.loss, CNN.accuracy],
feed_dict={CNN.X: self.X_test,
CNN.Y: self.Y_test})
We need now to train the model, evaluate it and test its performance on test data, and eventually include hyperparameters.
epochs = 100
batch_size = 100
n_filters = 10
n_neurons_connected = 50
n_categories = 10
eta_vals = np.logspace(-5, 1, 7)
lmbd_vals = np.logspace(-5, 1, 7)
CNN_tf = np.zeros((len(eta_vals), len(lmbd_vals)), dtype=object)
for i, eta in enumerate(eta_vals):
for j, lmbd in enumerate(lmbd_vals):
CNN = ConvolutionalNeuralNetworkTensorflow(X_train, Y_train, X_test, Y_test,
n_filters=n_filters, n_neurons_connected=n_neurons_connected,
n_categories=n_categories, epochs=epochs, batch_size=batch_size,
eta=eta, lmbd=lmbd)
CNN.fit()
print("Learning rate = ", eta)
print("Lambda = ", lmbd)
print("Test accuracy: %.3f" % CNN.test_accuracy)
print()
CNN_tf[i][j] = CNN
# visual representation of grid search
# uses seaborn heatmap, could probably do this in matplotlib
import seaborn as sns
sns.set()
train_accuracy = np.zeros((len(eta_vals), len(lmbd_vals)))
test_accuracy = np.zeros((len(eta_vals), len(lmbd_vals)))
for i in range(len(eta_vals)):
for j in range(len(lmbd_vals)):
CNN = CNN_tf[i][j]
train_accuracy[i][j] = CNN.train_accuracy
test_accuracy[i][j] = CNN.test_accuracy
fig, ax = plt.subplots(figsize = (10, 10))
sns.heatmap(train_accuracy, annot=True, ax=ax, cmap="viridis")
ax.set_title("Training Accuracy")
ax.set_ylabel("$\eta$")
ax.set_xlabel("$\lambda$")
plt.show()
fig, ax = plt.subplots(figsize = (10, 10))
sns.heatmap(test_accuracy, annot=True, ax=ax, cmap="viridis")
ax.set_title("Test Accuracy")
ax.set_ylabel("$\eta$")
ax.set_xlabel("$\lambda$")
plt.show()
import tensorflow as tf
from tensorflow.keras.layers import Input
from tensorflow.keras.models import Sequential #This allows appending layers to existing models
from tensorflow.keras.layers import Dense #This allows defining the characteristics of a particular layer
from tensorflow.keras import optimizers #This allows using whichever optimiser we want (sgd,adam,RMSprop)
from tensorflow.keras import regularizers #This allows using whichever regularizer we want (l1,l2,l1_l2)
from tensorflow.keras.utils import to_categorical #This allows using categorical cross entropy as the cost function
from tensorflow.keras.layers import Conv2D
from tensorflow.keras.layers import MaxPooling2D
from tensorflow.keras.layers import Flatten
def create_convolutional_neural_network_keras(input_shape, receptive_field,
n_filters, n_neurons_connected, n_categories,
eta, lmbd):
model = Sequential()
model.add(Conv2D(n_filters, (receptive_field, receptive_field), input_shape=input_shape, padding='same',
activation='relu', kernel_regularizer=l2(lmbd)))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Flatten())
model.add(Dense(n_neurons_connected, activation='relu', kernel_regularizer=l2(lmbd)))
model.add(Dense(n_categories, activation='softmax', kernel_regularizer=l2(lmbd)))
sgd = SGD(lr=eta)
model.compile(loss='categorical_crossentropy', optimizer=sgd, metrics=['accuracy'])
return model
epochs = 100
batch_size = 100
input_shape = X_train.shape[1:4]
receptive_field = 3
n_filters = 10
n_neurons_connected = 50
n_categories = 10
eta_vals = np.logspace(-5, 1, 7)
lmbd_vals = np.logspace(-5, 1, 7)
CNN_keras = np.zeros((len(eta_vals), len(lmbd_vals)), dtype=object)
for i, eta in enumerate(eta_vals):
for j, lmbd in enumerate(lmbd_vals):
CNN = create_convolutional_neural_network_keras(input_shape, receptive_field,
n_filters, n_neurons_connected, n_categories,
eta, lmbd)
CNN.fit(X_train, Y_train, epochs=epochs, batch_size=batch_size, verbose=0)
scores = CNN.evaluate(X_test, Y_test)
CNN_keras[i][j] = CNN
print("Learning rate = ", eta)
print("Lambda = ", lmbd)
print("Test accuracy: %.3f" % scores[1])
print()
# visual representation of grid search
# uses seaborn heatmap, could probably do this in matplotlib
import seaborn as sns
sns.set()
train_accuracy = np.zeros((len(eta_vals), len(lmbd_vals)))
test_accuracy = np.zeros((len(eta_vals), len(lmbd_vals)))
for i in range(len(eta_vals)):
for j in range(len(lmbd_vals)):
CNN = CNN_keras[i][j]
train_accuracy[i][j] = CNN.evaluate(X_train, Y_train)[1]
test_accuracy[i][j] = CNN.evaluate(X_test, Y_test)[1]
fig, ax = plt.subplots(figsize = (10, 10))
sns.heatmap(train_accuracy, annot=True, ax=ax, cmap="viridis")
ax.set_title("Training Accuracy")
ax.set_ylabel("$\eta$")
ax.set_xlabel("$\lambda$")
plt.show()
fig, ax = plt.subplots(figsize = (10, 10))
sns.heatmap(test_accuracy, annot=True, ax=ax, cmap="viridis")
ax.set_title("Test Accuracy")
ax.set_ylabel("$\eta$")
ax.set_xlabel("$\lambda$")
plt.show()