12.1. Assigning probabilities (I): Indifferences and translation groups

Discrete permutation invariance

• Consider a six-sided dice

• How do we assign \(p_i \equiv p(X_i|I)\), \(i \in \{1, 2, 3, 4, 5, 6\}\)?

• We do know \(\sum_i p(X_i|I) = 1\)

• Invariance under labeling \(\Rightarrow p(X_i|I)=1/6\)

  • provided that the prior information \(I\) says nothing that breaks the permutation symmetry (e.g., we might know that the dice are not fair).

Location invariance

Indifference to a constant shift \(x_0\) for a location parameter \(x\) implies that

(12.1)\[\begin{equation} p(x|I) dx \approx p(x+ x_0|I) d(x+x_0) = p(x+ x_0|I) dx, \end{equation}\]

in the allowed range.

Location invariance implies that

(12.2)\[\begin{equation} p(x|I) = p(x+ x_0|I) \quad \Rightarrow \quad p(x|I) = \mathrm{constant}. \end{equation}\]

• Provided that the prior information \(I\) says nothing that breaks the symmetry.

• The pdf will be zero outside the allowed range (specified by \(I\)).

Scale invariance

Indifference to a re-scaling \(\lambda\) of a scale parameter \(x\) implies that

(12.3)\[\begin{equation} p(x|I) dx \approx p(\lambda x|I) d(\lambda x) = \lambda p(\lambda x|I) dx, \end{equation}\]

in the allowed range.

Invariance under re-scaling implies that

(12.4)\[\begin{equation} p(x|I) = \lambda p(\lambda x|I) \quad \Rightarrow \quad p(x|I) \propto 1/x. \end{equation}\]

• Provided that the prior information \(I\) says nothing that breaks the symmetry.

• The pdf will be zero outside the allowed range (specified by \(I\)).

• This prior is often called a Jeffrey’s prior; it represents a complete ignorance of a scale parameter within an allowed range.

• It is equivalent to a uniform pdf for the logarithm: \(p(\log(x)|I) = \mathrm{constant}\)

  • as can be verified with a change of variable \(y=\log(x)\), see lecture notes on error propagation.

Checkpoint question

Can you provide alternative evidence for the scale invariance result?

Answer

scale invariance \(\longrightarrow\) \(p(x|I) \propto 1/x\)

• First check that it works: \(p(x|I) = \lambda p(\lambda x|I)\) \(\Lra\) \(\frac{c}{x} = \frac{\lambda c}{\lambda x} = \frac{c}{x}\). Check!

• Now a more general proof: assume \(p(x|I) \propto x^{\alpha}\). Then \(x^\alpha = \lambda (\lambda x)^{\alpha} = \lambda^{1+\alpha} x^\alpha\) \(\Lra\) \(\alpha = -1\). Check!

• Still more general: set \(\lambda = 1 + \epsilon\) with \(\epsilon \ll 1\), and solve to \(\mathcal{O}(\epsilon)\): \(p(x) = (1+\epsilon)(p(x)+\epsilon\frac{dp}{dx})\) \(\Lra\) \(p(x) + x \frac{dp}{dx} = 0\)

\[ \Lra \int_{p(x_0)}^{p(x)} \frac{dp}{p} = \int_{x_0}^x \frac{dx'}{x'} \ \Lra\ \log\frac{p(x)}{p(x_0)} = \log\frac{x_0}{x} \ \Lra\ p(x) = \left(\frac{p(x_0)}{x_0}\right)\frac{1}{x} \]

so \(p(x) \propto 1/x\).

Example: Straight-line model

Consider the theoretical model

(12.5)\[\begin{equation} y_\mathrm{th}(x) = \theta_1 x + \theta_0. \end{equation}\]

• Would you consider the intercept \(\theta_0\) a location or a scale parameter, or something else?

• Would you consider the slope \(\theta_1\) a location or a scale parameter, or something else?

Consider also the statistical model for the observed data \(y_i = y_\mathrm{th}(x_i) + \epsilon_i\), where we assume independent, Gaussian noise \(\epsilon_i \sim \mathcal{N}(0, \sigma^2)\).

• Would you consider the standard deviation \(\sigma\) a location or a scale parameter, or something else?

Symmetry invariance

• In fact, by symmetry indifference we could as well have written the linear model as \(x_\mathrm{th}(y) = \theta_1' y + \theta_0'\)

• We would then equate the probability elements for the two models

(12.6)\[\begin{equation} p(\theta_0, \theta_1 | I) d\theta_0 d\theta_1 = q(\theta_0', \theta_1' | I) d\theta_0' d\theta_1'. \end{equation}\]

• The transformation gives \((\theta_0', \theta_1') = (-\theta_1^{-1}\theta_0, \theta_1^{-1})\).

This change of variables implies that

(12.7)\[\begin{equation} q(\theta_0', \theta_1' | I) = p(\theta_0, \theta_1 | I) \left| \frac{d\theta_0 d\theta_1}{d\theta_0' d\theta_1'} \right|, \end{equation}\]

where the (absolute value of the) determinant of the Jacobian is

(12.8)\[\begin{equation} \left| \frac{d\theta_0 d\theta_1}{d\theta_0' d\theta_1'} \right| = \mathrm{abs} \left( \begin{vmatrix} \frac{\partial \theta_0}{\partial \theta_0'} & \frac{\partial \theta_0}{\partial \theta_1'} \\ \frac{\partial \theta_1}{\partial \theta_0'} & \frac{\partial \theta_1}{\partial \theta_1'} \end{vmatrix} \right) = \frac{1}{\left( \theta_1' \right)^3}. \end{equation}\]

• In summary we find that \(\theta_1^3 p(\theta_0, \theta_1 | I) = p(-\theta_1^{-1}\theta_0, \theta_1^{-1}|I).\)

• This functional equation is satisfied by

(12.9)\[\begin{equation} p(\theta_0, \theta_1 | I) \propto \frac{1}{\left( 1 + \theta_1^2 \right)^{3/2}}. \end{equation}\]

import matplotlib.pyplot as plt
import numpy as np

# straight line model with fixed intercept at y=x=0.
uniformSamples = np.random.uniform(size=100).reshape(1,-1)
priorSamplesSlope = {'uniform': 10*uniformSamples, #[0,10]
                         'scale': 10**(3*uniformSamples-2), #[0.01,10]
                         'symmetry': np.tan(np.arcsin(uniformSamples))}
xLinspace = np.array([0,1]).reshape(-1,1)

fig_slopeSamples, axs = plt.subplots(nrows=1,ncols=3,sharey=True, sharex=True)

for iax, (prior,slopes) in enumerate(priorSamplesSlope.items()):
    ax=axs[iax]
    ax.plot(xLinspace, xLinspace*slopes, color='k', alpha=0.1)
    ax.set_ylim(0,1)
    ax.set_xlabel(r'$x$')
    if ax.get_subplotspec().is_first_col():
        ax.set_ylabel(r'$y = \theta x$')
    ax.set_title(f'{prior} prior')

from myst_nb import glue
glue("slopeSamples_fig", fig_slopeSamples, display=False)

Show code cell output

Hide code cell output

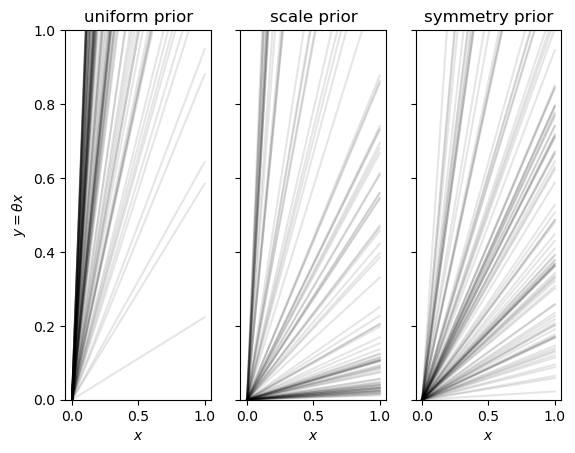
Fig. 12.1 100 samples of straight lines with fixed intercept equal to 0 and slopes sampled from three different prior pdfs. Note in particular the prior preference for large slopes that results from using a uniform pdf.