Gaussian Processes Exercises

Tasks include:

• building RBF kernels and visualizing samples,

• fitting a GP to 1D data (train/test split),

• plotting the posterior mean and ±2σ band,

• applying to a small dataset.

# Imports
import numpy as np
import matplotlib.pyplot as plt

from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, ConstantKernel as C, WhiteKernel
from sklearn.metrics import r2_score, mean_absolute_error

np.random.seed(1234)

# --- Kernel construction & draws from the prior ---
n = 200
X_demo = np.linspace(-2, 2, n).reshape(-1,1)
var, theta = 1.0, 0.2
kernel_demo = C(var) * RBF(length_scale=theta)

# Prior samples: draw f ~ GP(0, K) on the grid
from sklearn.metrics.pairwise import rbf_kernel
K = var * rbf_kernel(X_demo, X_demo, gamma=1.0/(2*theta**2))
samples = np.random.multivariate_normal(mean=np.zeros(n), cov=K + 1e-9*np.eye(n), size=3)

plt.figure(figsize=(8,6))
plt.plot(X_demo, samples.T, alpha=0.8)
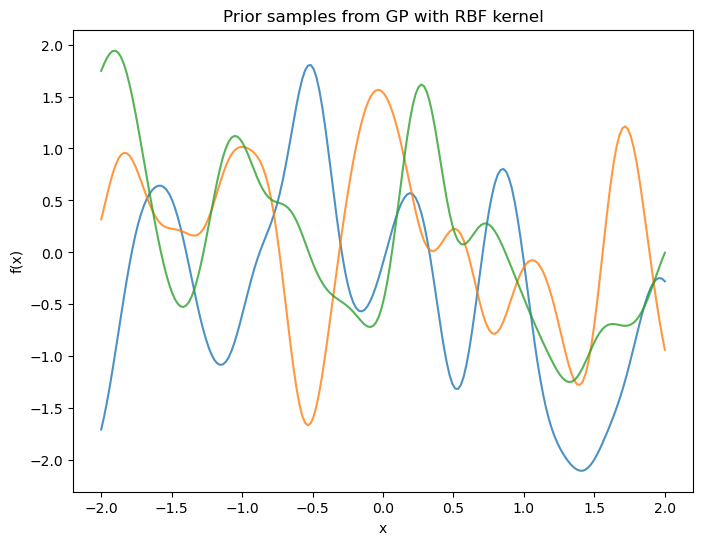
plt.title("Prior samples from GP with RBF kernel")
plt.xlabel("x"); plt.ylabel("f(x)")
plt.show()

# --- Fit GP on subset and predict on full grid ---
X = np.linspace(-2, 2, 60).reshape(-1,1)
f = np.sin(2*np.pi*X).ravel()
y = f + 0.25*np.random.randn(X.shape[0])

# Train/test split: every 3rd point for training to mimic original
idx = np.arange(X.shape[0])
mask_tr = (idx % 3 == 0)
mask_te = ~mask_tr
X_tr, y_tr = X[mask_tr], y[mask_tr]
X_te, y_te = X[mask_te], y[mask_te]

# Kernel: signal * RBF + noise
kernel = C(1.0, (1e-3, 1e3)) * RBF(length_scale=1.0, length_scale_bounds=(1e-3, 1e3)) + WhiteKernel(noise_level=1e-2, noise_level_bounds=(1e-6, 1e1))

gpr = GaussianProcessRegressor(kernel=kernel, normalize_y=True, n_restarts_optimizer=9, random_state=1234)
print("Initial kernel:", gpr.kernel)

gpr.fit(X_tr, y_tr)
print("\nOptimized kernel:", gpr.kernel_)

# Predict on full X (posterior mean/std)
y_mean, y_std = gpr.predict(X, return_std=True)

# Evaluate on held-out points
y_pred_te, y_std_te = gpr.predict(X_te, return_std=True)
print("\nTest R^2:", r2_score(y_te, y_pred_te))
print("Test MAE:", mean_absolute_error(y_te, y_pred_te))

# Plot
plt.figure(figsize=(8,6))
plt.fill_between(X.ravel(), y_mean-2*y_std, y_mean+2*y_std, alpha=0.2, label="±2σ")
plt.plot(X, y_mean, lw=2, label="GP mean")
plt.scatter(X_tr, y_tr, s=30, label="train")
plt.scatter(X_te, y_te, s=30, label="test", alpha=0.7)
plt.xlabel("x"); plt.ylabel("y")
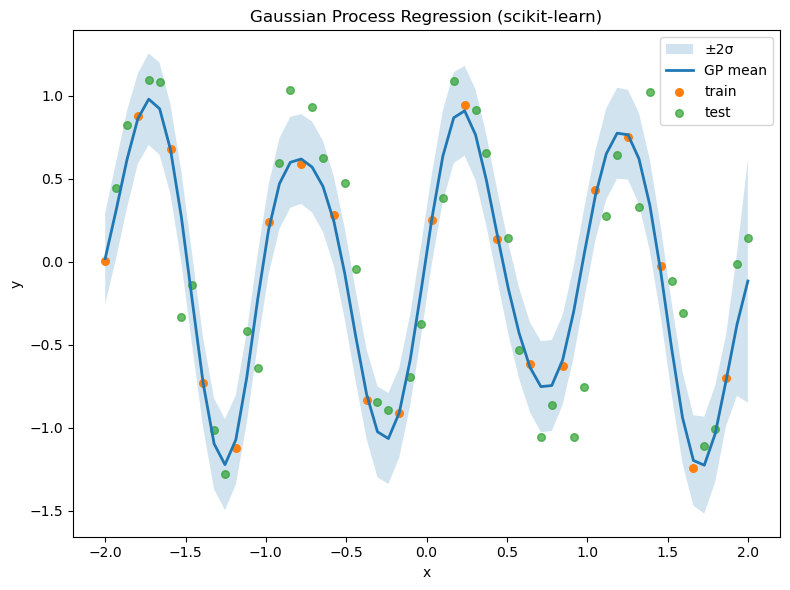
plt.title("Gaussian Process Regression (scikit-learn)")
plt.legend(); plt.tight_layout(); plt.show()

Initial kernel: 1**2 * RBF(length_scale=1) + WhiteKernel(noise_level=0.01)

Optimized kernel: 1.12**2 * RBF(length_scale=0.22) + WhiteKernel(noise_level=0.0204)

Test R^2: 0.7846195170516507
Test MAE: 0.28322738915095824

# --- Example dataset  ---

# Small inline sample approximating a downward trend (year vs pace)
years = np.array([1896,1900,1904,1908,1912,1920,1924,1928,1932,1936,1948,1952,1956,1960,1964,1968,1972,1976,1980,1984,1988,1992,1996,2000,2004,2008,2012,2016]).reshape(-1,1)
pace  = np.array([4.66,4.71,4.79,4.51,4.44,4.39,4.33,4.25,4.23,4.17,4.15,4.08,4.03,3.98,3.95,3.89,3.85,3.81,3.80,3.76,3.71,3.65,3.60,3.56,3.54,3.49,3.48,3.44])
Xo, Yo = years, pace

kernel_o = C(1.0, (1e-3, 1e3)) * RBF(length_scale=20.0, length_scale_bounds=(1e-1, 1e4))            + WhiteKernel(noise_level=1e-3, noise_level_bounds=(1e-6, 1e1))
gpr_o = GaussianProcessRegressor(kernel=kernel_o, normalize_y=True, n_restarts_optimizer=5, random_state=1234)

gpr_o.fit(Xo, Yo)
print("Optimized kernel (Olympic-like):", gpr_o.kernel_)

# Prediction grid
Xg = np.linspace(Xo.min()-4, Xo.max()+4, 400).reshape(-1,1)
Ym, Ys = gpr_o.predict(Xg, return_std=True)

plt.figure(figsize=(8,6))
plt.fill_between(Xg.ravel(), Ym-2*Ys, Ym+2*Ys, alpha=0.2, label="±2σ")
plt.plot(Xg, Ym, lw=2, label="GP mean")
plt.scatter(Xo, Yo, s=30, label="data")
plt.xlabel("year"); plt.ylabel("pace (min/km)")
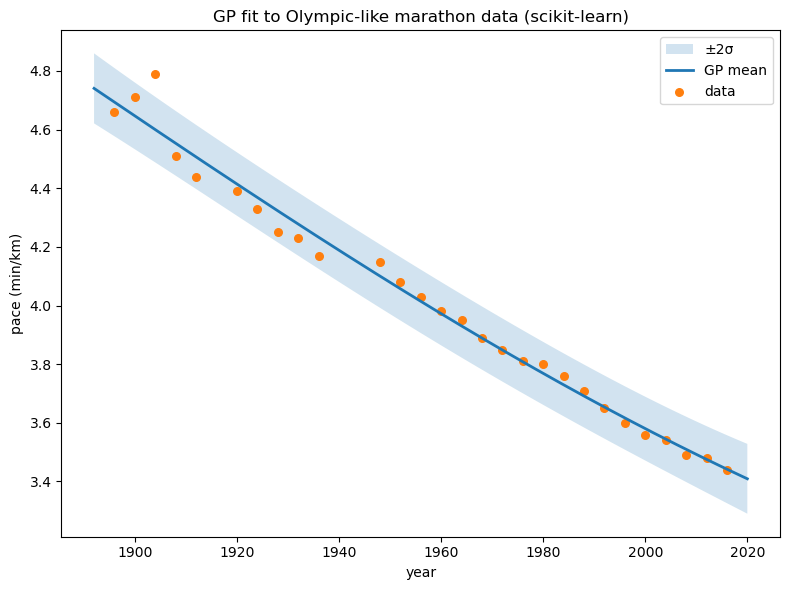
plt.title("GP fit to Olympic-like marathon data (scikit-learn)")
plt.legend(); plt.tight_layout(); plt.show()

Optimized kernel (Olympic-like): 5.22**2 * RBF(length_scale=277) + WhiteKernel(noise_level=0.0179)