20.3. The Zeus Ensemble Slice Sampler

From the documentation at the Zeus webpage:

• zeus is a Python implementation of the Ensemble Slice Sampling method.

  • Fast & Robust Bayesian Inference,

  • Efficient Markov Chain Monte Carlo (MCMC),

  • Black-box inference, no hand-tuning,

  • Excellent performance in terms of autocorrelation time and convergence rate,

  • Scale to multiple CPUs without any extra effort.

There are two relevant arXiv references for zeus:

1. Ensemble Slice Sampling: Parallel, black-box and gradient-free inference for correlated & multimodal distributions by Minas Karamanis and Florian Beutler.

2. zeus: A Python implementation of Ensemble Slice Sampling for efficient Bayesian parameter inference by Minas Karamanis, Florian Beutler, and John A. Peacock.

Fig. 20.2 Figure 1 from Ref. 1 above.

Fig. 20.3 Figure 2 from Ref. 2 above.

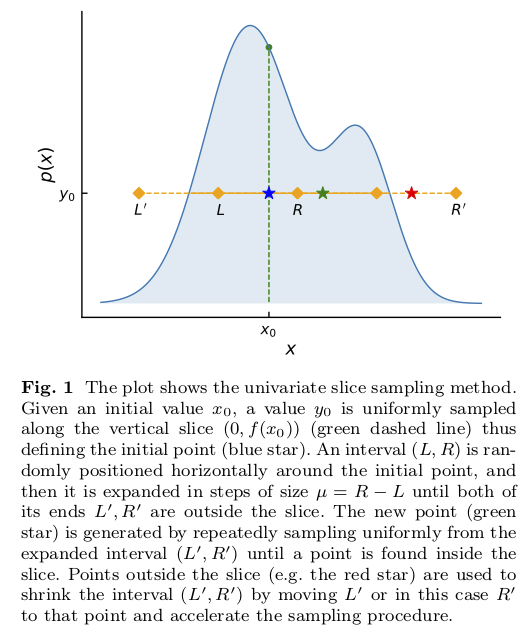
Slice sampling in action for a one-dimensional distribution is shown in Fig. 20.2. The idea is that sampling from a distribution \(p(x)\) is the same as uniform sampling from the area under the plot of \(f(x) \propto p(x)\). E.g., the highest probability \(p(x)\) is where the area is largest, and this is a simple proportionality. The height \(y\) is introduced with \(0 < y < f(x)\) as an auxiliary variable and one samples the uniform joint probability \(p(x,y)\). Then \(p(x)\) is obtained by marginalizing over \(y\) (meaning just dropping \(y\) from the sample).

The blue star comes from uniformly sampling in \(y\) at the initial point \(x_0\) to identify \(y_0\). The “slice” is the set of \(x\) such that \(y_0 < f(x)\). In the figure the interval initially from \(L\) to \(R\) is expanded to \(L'\) to \(R'\), which includes the full slice. When the final interval is found, a new \(x_1\) is drawn uniformly from the intersection of the interval and the slice. The green star is an accepted new point \(x_1\) (inside the slice) while the red star is a rejected point (outside the slice). There is one parameter to tune: the width \(\mu\) of the interval from \(L\) to \(R\) that sets the original interval around \(x_0\) and then the step size for expanding the interval to be from \(L'\) to \(R'\). In zeus the value of \(\mu\) is tuned by stochastic optimization.

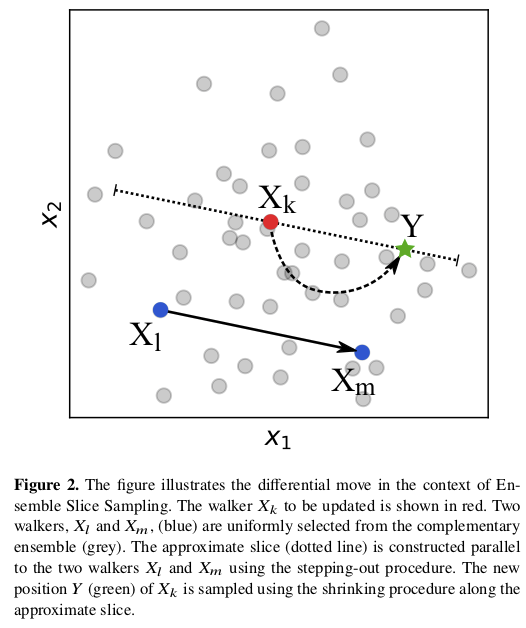
The “ensemble” aspect of zeus is that there are multiple walkers, as in the ensemble sampler emcee. Figure Fig. 20.3 illustrates how the ensemble of walkers is used to do what is called a “differential move”. There are several choices for moves, including a global one that is effective for multi-modal distributions. The basic call for zeus compared to emcee and PyMC is illustrated in Comparing samplers for a simple problem.

• An example from the zeus documentation of sampling from a multimodal distribution is given in .

• The text case for parallel tempering in a very simple multi-modal example is compared to zeus in