Exercise: Gaussian Processes

This exercise uses scikit-learn and covers:

• building RBF kernels with signal variance and length-scale,

• fitting GaussianProcessRegressor with a white-noise term,

• predicting posterior mean and uncertainty,

• plotting mean ±2σ and data,

• setting hyperparameters explicitly vs. optimizing by LML.

# Imports
import numpy as np
import matplotlib.pyplot as plt

from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, ConstantKernel as C, WhiteKernel
np.random.seed(1234)

# Synthetic 1D regression data (adapter-friendly)
# If your upstream notebook already defines X,y, this block can be skipped or adapted.
n = 75
X = np.linspace(-2, 2, n).reshape(-1,1)
f = np.sin(2*np.pi*X).ravel()
y = f + 0.15*np.random.randn(n)

print('Data shapes:', X.shape, y.shape)

Data shapes: (75, 1) (75,)

# Fixed hyperparameters (like setting m['rbf.lengthscale']=..., m['Gaussian_noise.variance']=...)
sigma_f2 = 1.0
ell = 0.2
sigma_n2 = 1e-2

kernel_fixed = C(sigma_f2, constant_value_bounds='fixed') * RBF(length_scale=ell, length_scale_bounds='fixed') \
               + WhiteKernel(noise_level=sigma_n2, noise_level_bounds='fixed')

gpr_fixed = GaussianProcessRegressor(kernel=kernel_fixed, normalize_y=True, optimizer=None)  # no optimization
gpr_fixed.fit(X, y)

Xg = np.linspace(X.min()-0.5, X.max()+0.5, 400).reshape(-1,1)
m_fixed, s_fixed = gpr_fixed.predict(Xg, return_std=True)

plt.figure(figsize=(8,6))
plt.fill_between(Xg.ravel(), m_fixed-2*s_fixed, m_fixed+2*s_fixed, alpha=0.2, label='±2σ')
plt.plot(Xg, m_fixed, lw=2, label='GP mean (fixed hyperparams)')
plt.scatter(X, y, s=25, label='data')
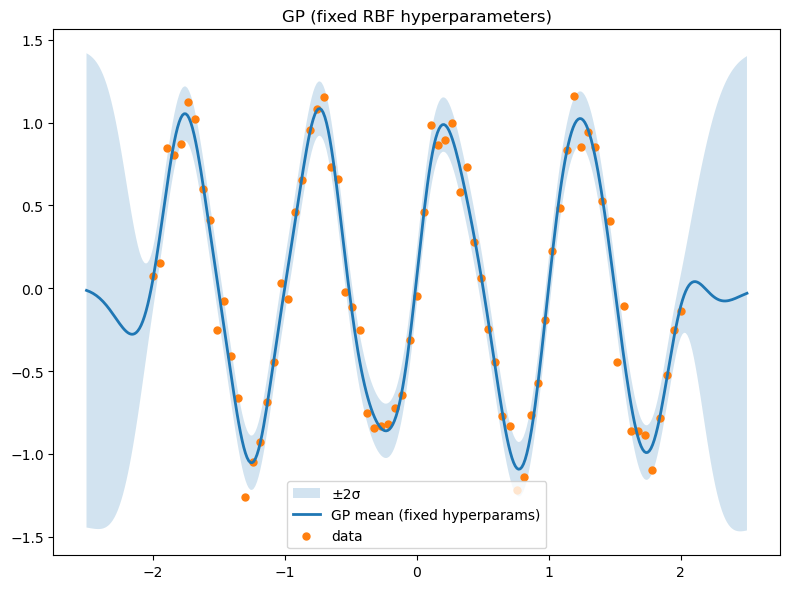
plt.title('GP (fixed RBF hyperparameters)')
plt.legend(); plt.tight_layout(); plt.show()

# Optimized hyperparameters (analog of m.optimize())
kernel0 = C(1.0, (1e-3, 1e3)) * RBF(length_scale=0.5, length_scale_bounds=(1e-3, 1e3)) \
          + WhiteKernel(noise_level=1e-2, noise_level_bounds=(1e-6, 1e1))

gpr = GaussianProcessRegressor(kernel=kernel0, normalize_y=True, n_restarts_optimizer=5, random_state=1234)
print('Initial kernel:', gpr.kernel)

gpr.fit(X, y)
print('\nOptimized kernel:', gpr.kernel_)

m_opt, s_opt = gpr.predict(Xg, return_std=True)

plt.figure(figsize=(8,6))
plt.fill_between(Xg.ravel(), m_opt-2*s_opt, m_opt+2*s_opt, alpha=0.2, label='±2σ')
plt.plot(Xg, m_opt, lw=2, label='GP mean (optimized)')
plt.scatter(X, y, s=25, label='data')
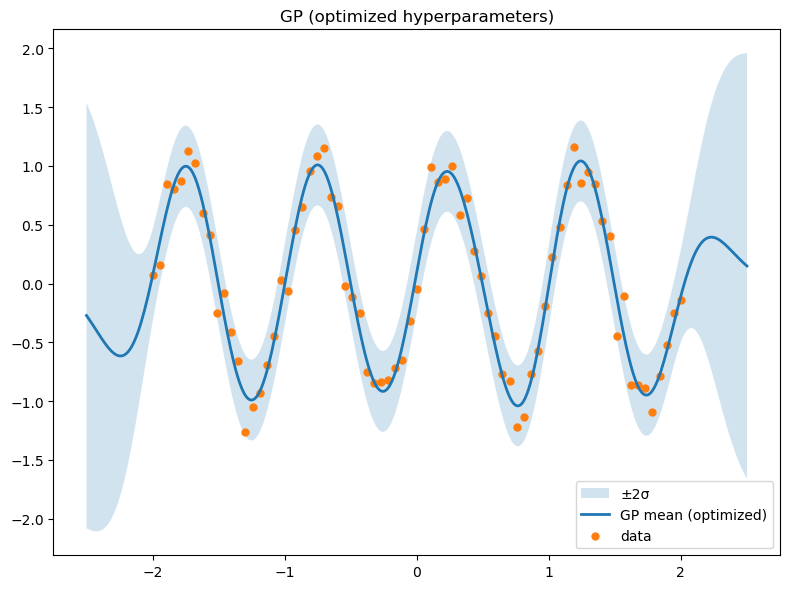
plt.title('GP (optimized hyperparameters)')
plt.legend(); plt.tight_layout(); plt.show()

Initial kernel: 1**2 * RBF(length_scale=0.5) + WhiteKernel(noise_level=0.01)

Optimized kernel: 1.31**2 * RBF(length_scale=0.277) + WhiteKernel(noise_level=0.0475)

# Optional: full predictive covariance 
m_cov, K_cov = gpr.predict(Xg, return_cov=True)
print('Predictive covariance shape:', K_cov.shape)

Predictive covariance shape: (400, 400)