Gaussian Process Regression

This notebook uses scikit-learn with the workflow:

• build an RBF-based kernel (with signal scale and noise term),

• fit the GP on a subset (e.g., every 3rd point),

• predict mean and uncertainty on a target grid or the full input,

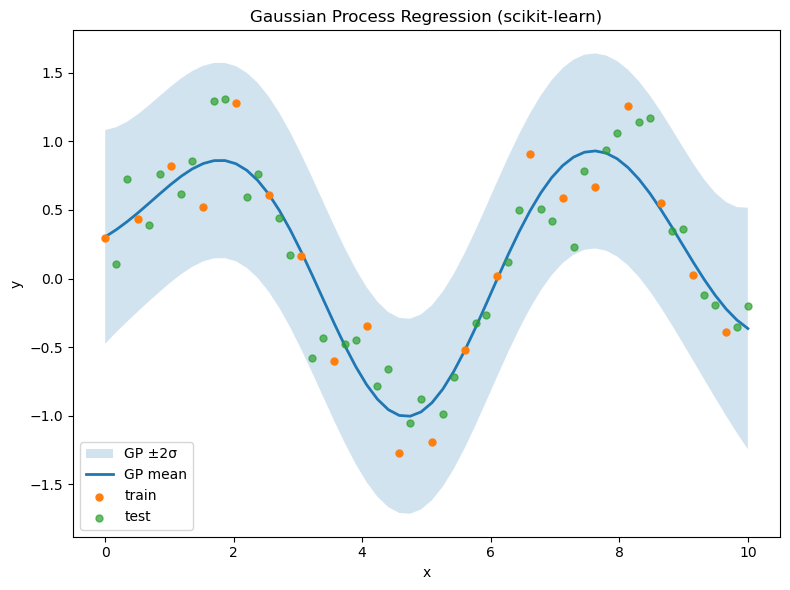
• plot mean ±2σ and data,

• compute simple validation metrics.

# Imports
import numpy as np
import matplotlib.pyplot as plt

from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, ConstantKernel as C, WhiteKernel

np.random.seed(1234)

x = np.linspace(0, 10, 60)
f = np.sin(x) + 0.2*np.cos(3*x)
y = f + 0.2*np.random.randn(x.size)

# Ensure shapes (n,1) and (n,)
X = np.asarray(x).reshape(-1, 1)
y = np.asarray(y).reshape(-1)
print('Data shapes -> X:', X.shape, ' y:', y.shape)

Data shapes -> X: (60, 1)  y: (60,)

# --- Train/validation split: every 3rd point for train ---
idx = np.arange(X.shape[0])
train_mask = (idx % 3 == 0)
test_mask  = ~train_mask

X_train, y_train = X[train_mask], y[train_mask]
X_test,  y_test  = X[test_mask],  y[test_mask]

print('Train size:', X_train.shape[0], ' Test size:', X_test.shape[0])

Train size: 20  Test size: 40

# --- Kernel: signal variance * RBF(length_scale) + white noise ---
kernel = C(1.0, (1e-3, 1e3)) * RBF(length_scale=1.0, length_scale_bounds=(1e-1, 1e3)) + WhiteKernel(noise_level=1e-3, noise_level_bounds=(1e-6, 1e1))

gpr = GaussianProcessRegressor(kernel=kernel, normalize_y=True, random_state=1234, n_restarts_optimizer=9)
print('Initial kernel:', gpr.kernel)

Initial kernel: 1**2 * RBF(length_scale=1) + WhiteKernel(noise_level=0.001)

# --- Fit (replaces GPy: m.optimize(...)) ---
gpr.fit(X_train, y_train)
print('\nOptimized kernel:', gpr.kernel_)

Optimized kernel: 1.03**2 * RBF(length_scale=1.36) + WhiteKernel(noise_level=0.193)

# --- Predict on full X (replaces: yp, vp = m.predict(xp)) ---
y_mean, y_std = gpr.predict(X, return_std=True)

# For test set metrics
from sklearn.metrics import r2_score, mean_absolute_percentage_error
y_pred_test, y_std_test = gpr.predict(X_test, return_std=True)
print('\nValidation:')
print('  R^2  (test):', r2_score(y_test, y_pred_test))
try:
    print('  MAPE (test):', mean_absolute_percentage_error(y_test, y_pred_test))
except Exception:
    pass

Validation:
  R^2  (test): 0.8596309559662871
  MAPE (test): 0.4463261384340149

# --- Plot (replaces: m.plot(...)) ---
plt.figure(figsize=(8,6))

# 95% confidence band
plt.fill_between(X.ravel(),
                 y_mean - 2*y_std,
                 y_mean + 2*y_std,
                 alpha=0.2, label='GP ±2σ')

plt.plot(X.ravel(), y_mean, lw=2, label='GP mean')
plt.scatter(X_train.ravel(), y_train, s=25, label='train', zorder=3)
plt.scatter(X_test.ravel(),  y_test,  s=25, label='test',  alpha=0.7, zorder=2)

plt.xlabel('x')
plt.ylabel('y')
plt.title('Gaussian Process Regression (scikit-learn)')
plt.legend()
plt.tight_layout()
plt.show()