Evidence for an expansion

Consider models \(M_1\) and \(M_2\), with the same dataset \(D\). For the evidence \(p(M_1|D,I)\) versus \(p(M_2|D,I)\) there is no reference to a particular parameter set \(\Lra\) it is a comparison between two models, not two fits. As already noted, in Bayesian model selection only a comparison makes sense. One does not deal with a hypothesis like: “Model \(M_1\) is correct.” Here we will eventually take \(M_2\) to be \(M_1\) with one extra order in an expansion (one additional parameter).

To proceed, as is often the case, we first apply Bayes’ theorem:

\[ \frac{p(M_2|D,I)}{p(M_1|D,I)} = \frac{p(D|M_2,I)p(M_2,I) / p(D|I)}{p(D|M_1,I) p(M_1,I) / p(D|I)} , \]

where the Bayes’ theorem denominators cancel. We’ll take the ratio \(p(M_ 2|I)/p(M_1,I)\) to be one. Thus we have:

(15.32)\[ \frac{p(M_2|D,I)}{p(M_1|D,I)} = \frac{\int d\avec_2\, p(D|\avec_2,M_2,I)p(\avec_2|M_2,I)} {\int d\avec_1\, p(D|\avec_1,M_1,I)p(\avec_1|M_1,I)} , \]

where we’ve made the usual application of the product rule in the marginalization integral in numerator and denominator. Note that the integration is over the entire parameter space. This is difficult numerically because likelihoods are usually peaked but can have long tails that contribute to the integral (cf. averaging over the likelihood vs. finding the peak).

Consider the easiest example: \(M_1 \rightarrow M_k\) and \(M_2 \rightarrow M_{k+1}\), where \(k\) is the order in an expansion. The question is then: Is going to a higher-order favored by the given data? To further simplify, assume \(M_{k+1}\) has one additional parameter \(a'\) and assume the priors factorize. For example they are Gaussians:

\[ e^{-\avec^2/2\bar{a}^2} = e^{-a_0^2/2\bar{a}^2}e^{-a_1^2/2\bar{a}^2} \cdots e^{-a_k^2/2\bar{a}^2} . \]

Then

\[ p(\avec_2|M_{k+1}, I) = p(\avec_1,a'|M_{k+1},I) = p(\avec_1|M_{k+1},I) p(a'|M_{k+1},I) \]

Consider cases …

i) values of \(a'\) that contribute to the integrand in the numerator of (15.32) are determined by the likelihood peaked region. E.g., recall

How can we approximate this? Take \(p(a'|M_{k+1},I)\)

Call the value of the likelihood peak \(\hat a\) and the width \(\delta a'\). So two different widths: the before-data \(\Delta a'\) (width of prior) and the after-data \(\delta a'\) (likelihood \(\rightarrow\) posterior). Do the \(a'\) integral:

\[ \Lra \frac{p(D|M_{k+1},I)}{p(D|M_k)} \approx \frac{\delta a'}{\Delta a'} \frac{\int d\avec_1\, p(D|\avec_1,\hat a', M_{k+1},I) p(\avec_1|M_{k+1}, I)} {\int d\avec_1\, p(D|\avec_1,M_{k},I) p(\avec_1|M_{k}, I)} \]

with \(\delta a'\) from the integral over \(a'\) (leaving the peak value \(\hat a'\) in the numerator integral over \(\avec_1\)) and \(\Delta a'\) from \(p(a'|M_{k+1},I)\).

Therefore the ratio of the integrals is the gain in the likelihood from an extra parameter with value \(\hat a\) (cf. \(M_{k+1}(\hat a'=0) = M_k\)). But also the “Occam factor” or “Occam penalty” \(\delta a'/\Delta a'\). How much parameter space collapses in the face of data? We thought initially that \(a'\) could be anywhere in \(\Delta a'\), but find after seeing the data that it is only in \(\delta a'\). What a waste (less predictive) if \(\delta a' \ll \Delta a'\)! These factors play off each other: if we add a parameter to a nested model, we expect to gain because \(\hat a'\) is more information (it could be \(a'=0\) instead).

Now if this is the case:

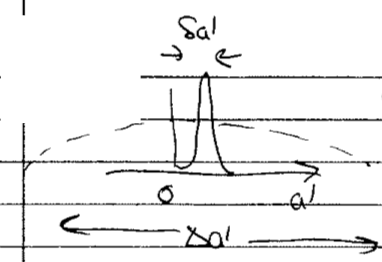
The \(a'=0\) likelihood is \(\ll\) the \(a'=\hat a'\) likelihood \(\Lra\) evidence ratio \(\gg 1\) and inclusion of this parameter is highly favored. Unless you put a flat prior from near \(-\infty\) to near \(+\infty\). But we have a natural prior, so \(\Delta a'\) is restricted.

ii) Now suppose:

Turn the analysis on its head. The dependence on \(a'\) is weak because of the width of the likelihood, so we can replace it in \(p(D|\avec_1,a',M_{k+1},I)\) by \(\hat a\):

\[ \Lra \frac{p(D|M_{k+1},I)}{p(D|M_k)} \approx \frac{\int d\avec_1\, p(D|\avec_1,\hat a', M_{k+1},I) p(\avec_1|M_{k+1}, I) \int da' p(a'|M_{k+1}, I)} {\int d\avec_1\, p(D|\avec_1,M_{k},I) p(\avec_1|M_{k}, I)} \]

The second integral in the numerator is now just a normalization integral, so it yields one. Further, we can take \(\hat a' \approx 0\) because we are dominated by the prior. But \(M_{k+1}\) with \(\hat a'=0\) is \(M_k\)! This means that the Bayes ratio in this situation goes to one rather than decreasing. The same argument applies to \(k+1 \rightarrow k_2 \rightarrow \ldots\) \(\Lra\) we have saturation of the \(a_k\)’s.

Summary: a naturalness prior cuts down on wasted space in the parameter phase space that might be ruled out by data. Thus an EFT is a simpler model (in the model selection sense) than the same functional form with uncontrained or only weakly constrained LECs.

Checkpoint question

Predict based on your own experience: How does this behavior change if we have more data (higher energy) or more certain data?

Answer

[fill in your own answer!]

Evidence with linear algebra

Return to the notebook to look at the calculation of evidence with Python linear algebra. The integrals to calculate are Gaussian in multiple variables: \(\avec = (a_0, \ldots, a_k)\) plus \(\bar{a}\). We can write them with matrices:

\[ \chi^2 = [Y - A\thetavec]^\intercal\, \Sigmavec^{-1}\, [Y - A\thetavec] , \]

where

\[\begin{split} Y - A\thetavec = \underbrace{\pmatrix{y_1 \\ y_2 \\ \vdots \\ y_N}}_{N\times 1} - \underbrace{\pmatrix{1 & x_1 & x_1^2 & \cdots & x_1^k \\ 1 & x_2 & x_2^2 & \cdots & x_2^k \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 1 & x_N & x_N^2 & \cdots & x_N^k}}_{N\times (k+1)} \underbrace{\pmatrix{a_0 \\ a_1 \\ a_2 \\ \vdots \\ a_k}}_{(k+1)\times 1} \end{split}\]

and

\[\begin{split} \Sigma = \underbrace{\pmatrix{\sigma_{1}^2 & \rho_{12}\sigma_{1}\sigma_{y_2} & \cdots & \rho_{1N}\sigma_{1}\sigma_{N} \\ & \sigma_{2}^2 & \cdots & \cdots \\ & & \ddots & \cdots \\ & & & \sigma_{N}^2 }}_{N\times N} . \end{split}\]

Then from before we have \(\chi^2_{\text{MLE}}\) when

\[ \widehat\thetavec = (A^\intercal \Sigma^{-1} A)^{-1}(A^\intercal \Sigma^{-1} Y) . \]

Here we have a couple of options:

i) Use

\[ \int e^{-\frac{1}{2}x^\intercal M x + \Bvec^\intercal x} dx = \sqrt{\det(2\pi M^{-1})} e^{\frac{1}{2}\Bvec^\intercal M^{-1} \Bvec} \]

where \(M\) is any symmetric matrix and \(\Bvec\) any vector. Derive this result by completing the square in the exponent (subtract and add \(\frac{1}{2}\Bvec^\intercal M^{-1} \Bvec\)).

ii) Use conjugacy. See the “conjugate prior” entry in Wikipedia for details. Apply this to Bayes’ theorem with a Gaussian prior \(p(\thetavec)\) with \((\mu_0,\sigma_0)\) and a Gaussian likelihood \(p(D|\thetavec)\) with \((\mu,\sigma)\). Then \(p(\thetavec|D)\) is a Gaussian with

\[ \tilde\mu = \frac{1}{\frac{1}{\sigma_0^2} + \frac{N}{\sigma^2}} \left(\frac{\mu_0}{\sigma_0^2}+ \frac{\sum_{i=1}^{N}y_i}{\sigma^2}\right) \qquad \tilde\sigma^2 = \left(\frac{1}{\sigma_0^2} + \frac{N}{\sigma^2}\right)^{-1} \]

Checkpoint question

Check the \(N\rightarrow \infty\) limit

Answer

Then the terms with \(\mu_0\) and \(\sigma_0\) become negligible, and

\[ \tilde\mu \underset{N\rightarrow\infty}{\longrightarrow} \frac{1}{N}\sum_{i=1}^{N}y_i \qquad \tilde\sigma^2 \underset{N\rightarrow\infty}{\longrightarrow} \sigma^2 / N . \]