23. Logistic Regression

In linear regression our main interest was centered on learning the coefficients of a functional fit (say a polynomial) in order to be able to predict the response of a continuous variable on some unseen data. The fit to the continuous variable \(y^{(i)}\) is based on some independent variables \(\boldsymbol{x}^{(i)}\). Linear regression resulted in analytical expressions for standard ordinary Least Squares or Ridge regression (in terms of matrices to invert) for several quantities, ranging from the variance and thereby the confidence intervals of the parameters \(\boldsymbol{w}\) to the mean squared error. If we can invert the product of the design matrices, linear regression gives then a simple recipe for fitting our data.

Classification problems, however, are concerned with outcomes taking the form of discrete variables (i.e. categories). We may for example, on the basis of DNA sequencing for a number of patients, like to find out which mutations are important for a certain disease; or based on scans of various patients’ brains, figure out if there is a tumor or not; or given a specific physical system, we’d like to identify its state, say whether it is an ordered or disordered system (typical situation in solid state physics); or classify the status of a patient, whether she/he has a stroke or not and many other similar situations.

The most common situation we encounter when we apply logistic regression is that of two possible outcomes, normally denoted as a binary outcome, true or false, positive or negative, success or failure etc.

23.1. Optimization and Deep learning

Logistic regression will also serve as our stepping stone towards neural network algorithms and supervised deep learning. For logistic learning, the minimization of the cost function leads to an optimization problem that is non-linear in the parameters \(\boldsymbol{w}\). This optimization (how to find reliable minima of a multi-variable function) is a key challenge for all machine learning algorithms. This leads us back to the family of gradient descent methods encountered in the chapter on Mathematical optimization. These methods are the working horses of basically all modern machine learning algorithms.

We note also that many of the topics discussed here on logistic regression are also commonly used in modern supervised deep learning models, as we will see later.

23.2. Basics and notation

We consider the case where the dependent variables (also called the responses, targets, or outcomes) are discrete and only take values from \(k=1, \dots, K\) (i.e. \(K\) classes).

The goal is to predict the output classes from the design matrix \(\boldsymbol{X}\in\mathbb{R}^{n\times p}\) made of \(n\) samples, each of which carries \(p\) features or predictors. The primary goal is to identify the classes to which new unseen samples belong.

Notation

We will use the following notation:

• \(\boldsymbol{x}\): independent (input) variables, typically a vector of length \(p\). A matrix of \(N\) instances of input vectors is denoted \(\boldsymbol{X}\), and is also known as the design matrix. The input for machine-learning applications are often referred to as features.

• \(t\): dependent, response variable, also known as the target. For binary classification the target \(t^{(i)} \in \{0,1\}\). For \(K\) different classes we would have \(t^{(i)} \in \{1, 2, \ldots, K\}\). A vector of \(N\) targets from \(N\) instances of data is denoted \(\boldsymbol{t}\).

• \(\mathcal{D}\): is the data, where \(\mathcal{D}^{(i)} = \{ (\boldsymbol{x}^{(i)}, t^{(i)} ) \}\).

• \(\boldsymbol{y}\): is the output of our classifier that will be used to quantify probabilities \(p_{t=C}\) that the target belongs to class \(C\).

• \(\boldsymbol{w}\): will be the parameters (weights) of our classification model.

23.3. Binary classification

Let us specialize to the case of two classes only, with outputs \(t^{(i)} \in \{0,1\}\). That is

(23.1)\[\begin{equation} t^{(i)} = \begin{bmatrix} 0 \\ 1 \end{bmatrix} = \begin{bmatrix} \mathrm{no}\\ \mathrm{yes} \end{bmatrix}. \end{equation}\]

The perceptron

Before moving to the logistic model, let us try to use a linear regression model to classify these two outcomes. We could use a linear model

(23.2)\[\begin{equation} \boldsymbol{\tilde{y}} = \boldsymbol{X} \boldsymbol{w}, \end{equation}\]

where \(\boldsymbol{\tilde{y}}\) is a vector representing the possible outcomes, \(\boldsymbol{X}\) is our \(n\times p\) design matrix and \(\boldsymbol{w}\) are the model parameters.

Note however that our outputs \(\tilde{y}^{(i)} \in \mathbb{R}\) take values on the entire real axis. Our targets \(t^{(i)}\), however, are discrete variables.

One simple way to get a discrete output is to have sign functions that map the output of a linear regressor to values \(y^{(i)} \in \{ 0, 1 \}\), \(y^{(i)} = f(\tilde{y}^{(i)})=\frac{\mathrm{sign}(\tilde{y}^{(i)})+1}{2}\), which will map to one if \(\tilde{y}^{(i)}\ge 0\) and zero otherwise. Historically this model is called the perceptron in the machine learning literature.

The perceptron is an example of a “hard classification” model. We will encounter this model when we discuss neural networks as well. Each datapoint is deterministically assigned to a category (i.e \(y^{(i)}=0\) or \(y^{(i)}=1\)). In many cases, it is favorable to have a soft classifier that outputs the probability of a given category rather than a single value. For example, given \(\boldsymbol{x}^{(i)}\), the classifier outputs the probability of being in a category \(k\).

The logistic function

Logistic regression is the simplest example of the use of such a soft classifier. Let us assume that we have two classes such that \(t^{(i)}\) is either \(0\) or \(1\).

In logistic regression, we will use the so-called logit function

(23.3)\[\begin{equation} y(\boldsymbol{x}; \boldsymbol{w}) = y(z) = \frac{1}{1+e^{-z}} = \frac{e^z}{1+e^z}, \end{equation}\]

with the so called activation \(z = z(\boldsymbol{x}; \boldsymbol{w})\). This function is no longer linear in the model parameters \(\boldsymbol{w}\). It is an example of a S-shape or Sigmoid function.

We let \(y^{(i)}\) give the probability that a data point \(\boldsymbol{x}^{(i)}\) belongs to category \(t^{(i)} = 1\),

(23.4)\[\begin{equation} \prob \left( t^{(i)} = 1 \vert \boldsymbol{x}^{(i)}, \boldsymbol{w} \right) = y(\boldsymbol{x}^{(i)}; \boldsymbol{w}). \end{equation}\]

• Most frequently one uses \(z = z(\boldsymbol{x}, \boldsymbol{w}) \equiv \boldsymbol{x} \cdot \boldsymbol{w}\).

• It is common to introduce also a bias, or threshold, weight \(w_0\). This can be accommodated by prepending a constant feature \(x_0^{(i)}=1\) for all \(i\).

• Note that \(1-y(z)= y(-z)\).

• The sigmoid function can be motivated in several different ways:

  • In information theory this function represents the probability of a signal \(s=1\) rather than \(s=0\) when transmission occurs over a noisy channel.

  • It can be seen as an artificial neuron that mimics aspects of its biological counterpart.

Standard activation functions

Show code cell content

Hide code cell content

import numpy as np
import matplotlib.pyplot as plt
from myst_nb import glue

# Set the relevant activation interval 
z = np.linspace(-6,6,num=1201)

# Perceptron model
def y_perceptron(z):
    return (np.sign(z)+1)/2
    
# logit model
def y_logit(z):
    return 1 / (1+np.exp(-z))
    
# tanh model
def y_tanh(x):
    return (np.tanh(z)+1)/2
    
    
# Create a visualization
fig, ax = plt.subplots(nrows=1, ncols=1, sharey=True, **{"figsize":(6,4)})
ax.plot(z,y_perceptron(z),label='perceptron',lw=2,ls='-.',color='red')
ax.plot(z,y_logit(z),label='logit',lw=2,ls='-',color='blue')
ax.plot(z,y_tanh(z),label='tanh (normalized)',lw=2,ls='--',color='black')
ax.legend(loc='best')
ax.set_xlabel(r'Activation $z$')
ax.set_ylabel('Activation function')

glue("sigmoid_functions_fig", fig, display=False)

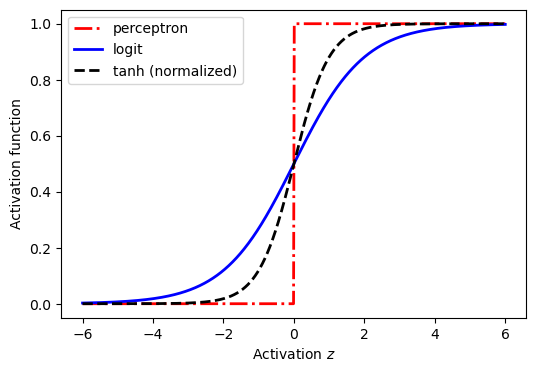
Fig. 23.1 The sigmoid, step,and (normalized) tanh functions; three common classifier functions used in classification and neural networks. In these lecture notes we use the letter \(z\) to denote the activation.

A binary classifier with two parameters

We assume now that we have two classes with \(t^{(i)}\) being either \(0\) or \(1\). Furthermore we assume also that we have only two parameters \(w_0, w_1\) and the features \(\boldsymbol{x}^{(i)} = \{ 1, x^{(i)} \}\) defining the activation function. I.e., there is a single independent (input) variable \(x\). We can produce probabilities from the classifier output \(y^{(i)}\)

\[\begin{align*} \prob (t^{(i)}=1|x^{(i)},\boldsymbol{w}) &= y(z^{(i)})= \frac{\exp{(w_0+w_1x^{(i)})}}{1+\exp{(w_0+w_1x^{(i)})}},\\ \prob (t^{(i)}=0|x^{(i)},\boldsymbol{w}) &= 1 - \prob (t^{(i)}=1|x^{(i)},\boldsymbol{w}) = \frac{1}{1+\exp{(w_0+w_1x^{(i)})}}, \end{align*}\]

where \(\boldsymbol{w} = ( w_0, w_1)\) are the weights we wish to extract from training data.

Determination of weights

Among ML practitioners, the prevalent approach to determine the weights in the activation function(s) is by minimizing some kind of cost function using some version of gradient descent. As we will see this usually corresponds to maximizing a likelihood function with or without a regularizer.

In this course we will obviously also advocate (or at least make aware of) the more probabilistic approach to learning about these parameters.

Maximum likelihood

In order to define the total likelihood for all possible outcomes from a dataset \(\mathcal{D}=\{(x^{(i)}, t^{(i)},)\}\), with the binary labels \(t^{(i)}\in\{0,1\}\) and where the data points are drawn independently, we use the binary version of the Maximum Likelihood Estimation (MLE) principle. We express the likelihood in terms of the product of the individual probabilities of a specific outcome \(t^{(i)}\), that is

\[\begin{align*} \mathcal{L} = \prob (\mathcal{D}|\boldsymbol{w})& = \prod_{i=1}^N \left[p(t^{(i)}=1|x^{(i)},\boldsymbol{w})\right]^{t^{(i)}}\left[1-p(t^{(i)}=1|x^{(i)},\boldsymbol{w}))\right]^{1-t^{(i)}}\nonumber \\ \end{align*}\]

The cost/loss function (to be minimized) is then defined as the negative log-likelihood

(23.5)\[\begin{equation} \mathcal{C}(\boldsymbol{w}) = -L \equiv -\log(\mathcal{L}) = -\sum_{i=1}^N \left( t^{(i)}\log{\prob (t^{(i)}=1|x^{(i)},\boldsymbol{w})} + (1-t^{(i)})\log\left[1-\prob (t^{(i)}=1|x^{(i)},\boldsymbol{w}))\right]\right). \end{equation}\]

The cost function rewritten as cross entropy

Using the definitions of the probabilities we can rewrite the cost/loss function as

(23.6)\[\begin{equation} \mathcal{C}(\boldsymbol{w}) = -\sum_{i=1}^N \left( t^{(i)}\log{ y(x^{(i)},\boldsymbol{w})} + (1-t^{(i)})\log\left[ 1-y( x^{(i)},\boldsymbol{w}) \right] \right), \end{equation}\]

which can be recognised as the relative entropy between the empirical probability distribution \((t^{(i)}, 1-t^{(i)})\) and the probability distribution predicted by the classifier \((y^{(i)}, 1-y^{(i)})\). Therefore, this cost function is known in statistics as the cross entropy.

Using specifically the logistic sigmoid activation function with two weights, and reordering the logarithms, we can rewrite the log-likelihood to obtain

(23.7)\[\begin{equation} \mathcal{C}(\boldsymbol{w})=-\sum_{i=1}^N \left[ t^{(i)} (w_0+w_1x^{(i)}) -\log{ \left( 1+\exp{(w_0+w_1x^{(i)})} \right) } \right]. \end{equation}\]

MLE should give the weights \(\boldsymbol{w}^*\) that minimizes this cost function.

Regularization

In practice, just as for linear regression, one often supplements the cross-entropy cost function with additional regularization terms, usually \(L_1\) and \(L_2\) regularization. This introduces hyperparameters into the classifier.

In particular, Ridge regularization is obtained by defining another cost function

(23.8)\[\begin{equation} \mathcal{C}_W (\boldsymbol{w}) \equiv \mathcal{C} (\boldsymbol{w}) + \alpha E_W (\boldsymbol{w}) \end{equation}\]

where \(E_W (\boldsymbol{w}) = \frac{1}{2} \sum_j w_j^2\) and \(\alpha\) is known as the weight decay.

Question

Can you motivate why \(\alpha\) is known as the weight decay?

Hint: Recall the origin of this regularizer from a Bayesian perspective.

Minimizing the cross entropy

The cross entropy is a convex function of the weights \(\boldsymbol{w}\) and, therefore, any local minimizer is a global minimizer.

Minimizing this cost function (here without regularization term) with respect to the two parameters \(w_0\) and \(w_1\) we obtain

\[\begin{align*} \frac{\partial \mathcal{C}(\boldsymbol{w})}{\partial w_0} &= -\sum_{i=1}^N \left(t^{(i)} -\frac{\exp{(w_0+w_1x^{(i)})}}{1+\exp{(w_0+w_1x^{(i)})}}\right) &= -\sum_{i=1}^N \left(t^{(i)} - y^{(i)} \right), \\ \frac{\partial \mathcal{C}(\boldsymbol{w})}{\partial w_1} &= -\sum_{i=1}^N \left(t^{(i)} x^{(i)} -x^{(i)}\frac{\exp{(w_0+w_1x^{(i)})}}{1+\exp{(w_0+w_1x^{(i)})}}\right) &= -\sum_{i=1}^N x^{(i)} \left(t^{(i)} - y^{(i)} \right). \end{align*}\]

A more compact expression

Let us now define a vector \(\boldsymbol{t}\) with \(n\) elements \(t^{(i)}\), an \(N\times 2\) matrix \(\boldsymbol{X}\) which contains the \((1, x^{(i)})\) predictor variables, and a vector \(\boldsymbol{y}\) of the outputs \(y^{(i)} = y(x^{(i)},\boldsymbol{w})\). We can then express the first derivative of the cost function in matrix form

(23.9)\[\begin{equation} \frac{\partial \mathcal{C}(\boldsymbol{w})}{\partial \boldsymbol{w}} = -\boldsymbol{X}^T\left( \boldsymbol{t}-\boldsymbol{y} \right). \end{equation}\]

A learning algorithm

Notice. Having access to the first derivative we can define an on-line learning rule as follows:

• For each input \(i\) (possibly permuting the sequence in each epoch) compute the error \(e^{(i)} = t^{(i)} - y^{(i)}\).

• Adjust the weights in a direction that would reduce this error: \(\Delta w_j = \eta e^{(i)} x_j^{(i)}\). The parameter \(\eta\) is called the learning rate.

• Perform multiple passes through the data, where each pass is known as an epoch. The computation of outputs \(\boldsymbol{y}\) given a set of weights \(\boldsymbol{w}\) is known as a forward pass, while the computation of gradients and adjustment of weights is called back-propagation.

You will recognise this learning algorithm as stochastic gradient descent.

Alternatively, one can perform batch learning for which multiple instances are combined into a batch, and the weights are adjusted following the matrix expression stated above. At the end, one hopes to have reached an optimal set of weights.

Extending to more features

Within a binary classification problem, we can easily expand our model to include multiple input features. Our activation function is then (with \(p\) features)

(23.10)\[\begin{equation} z( \boldsymbol{x}^{(i)}, \boldsymbol{w} ) = w_0 + w_1 x_1^{(i)} + w_2 x_2^{(i)} + \dots + w_p x_p^{(i)}. \end{equation}\]

Defining \(\boldsymbol{x}^{(i)} \equiv [1,x_1^{(i)}, x_2^{(i)}, \dots, x_p^{(i)}]\) and \(\boldsymbol{w}=[w_0, w_1, \dots, w_p]\) we get

(23.11)\[\begin{equation} \prob (t^{(i)}=1 | \boldsymbol{w}, \boldsymbol{x}^{(i)}) = \frac{ \exp{ \left( \boldsymbol{w} \cdot \boldsymbol{x}^{(i)} \right) }}{ 1 + \exp{ \left( \boldsymbol{w} \cdot \boldsymbol{x}^{(i)} \right) } }. \end{equation}\]

23.4. Extending to more classes

Until now we have focused on binary classification involving just a decision between two classes. Suppose we wish to extend to \(K\) classes. We will then introduce \(K\) outputs \(\boldsymbol{y}^{(i)} = \{ y_1^{(i)}, y_2^{(i)}, \ldots, y_{K}^{(i)} \}\).

Question

Actually, we would only need \(K-1\) outputs to create a soft classifier for \(K\) classes. Why?

Let us for the sake of simplicity assume we have only one feature. The activations are (suppressing the index \(i\))

(23.12)\[\begin{equation} z_1 = w_{1,0}+w_{1,1}x_1, \end{equation}\]

(23.13)\[\begin{equation} z_2 = w_{2,0}+w_{2,1}x_1, \end{equation}\]

and so on until the class \(K\):th class

(23.14)\[\begin{equation} z_{K} = w_{K,0}+w_{K,1}x_1, \end{equation}\]

and the model is specified in term of \(K\) so-called log-odds or logit transformations \(y_j^{(i)} = y(z_j^{(i)})\).

Class probabilities: The Softmax function

The transformation of the multiple outputs, as described above, to probabilities for belonging to any of \(K\) different classes can be achieved via the so-called Softmax function.

The Softmax function is used in various multiclass classification methods, such as multinomial logistic regression (also known as softmax regression), multiclass linear discriminant analysis, naive Bayes classifiers, and artificial neural networks. Specifically, the predicted probability for the \(k\):th class given a sample vector \(\boldsymbol{x}^{(i)}\) and a weighting vector \(\boldsymbol{w}\) is (with one independent variable):

(23.15)\[\begin{equation} \prob (t^{(i)}=k\vert \boldsymbol{x}^{(i)}, \boldsymbol{w} ) = \frac{\exp{(w_{k,0}+w_{k,1}x_1^{(i)})}} {\sum_{l=1}^{K}\exp{(w_{l,0}+w_{l,1}x_1^{(i)})}}. \end{equation}\]

which means that the discrete set of probabilities is properly normalized.

Our earlier discussions were all specialized to the case with two classes only. It is easy to see from the above that what we derived earlier is compatible with these equations.